Теперь у нас есть все необходимые знания, чтобы изучить очень важное явление интерференции световых волн, то явление, которое успешно исследовал Томас Юнг на рубеже XVIII и XIX веков с целью устранить давнее противоречие в объяснении природы света. Это противоречие тесно связано с именем Ньютона, который проводил обширные исследования оптических эффектов. Большая часть оптических исследований Ньютона начиналась в годы[52], проведенные им вдали от Кембриджа, отрезанного от него чумой. Именно эти годы привели Ньютона к созданию знаменитых “ Принципов…” [53]. Ньютон своим авторитетом почти на 100 лет утвердил теорию, которая рассматривала свет как поток крошечных частиц. Гюйгенс же придерживался волновой теории света. Хотя достоверных результатов, доступных во времена Ньютона и Гюйгенса явно не хватало, чтобы предпочесть одну теорию другой, нужно признать, что точка зрения Гюйгенса даже тогда казалась более убедительной. Однако престиж имени Ньютона был таков, что очень немногие физики XVIII века решались отказаться от ньютоновской корпускулярной [54] теории света, несмотря на растущую очевидность того, что такие явления как дифракция и постоянство скорости света легко объясняются волновой теорией, но выглядят неестественно для потока частиц.
Томас Юнг, чьи работы стали окончательным “ ударом милосердия [55] “ по точке зрения Ньютона, был человеком разносторонних талантов. В зените своей научной карьеры он оставил должность профессора натурфилософии Лондонского Королевского института, чтобы продолжить медицинскую практику[56]. В поздний период своей жизни Юнг увлеченно занимался расшифровкой древнеегипетских иероглифов в текстах на Розеттском камне [57].
Эксперимент, который выбрал Юнг, был связан с интерференцией света на двух щелях. Проще всего объяснить суть опыта Юнга на рисунке, который напомнит нам рассмотренный выше пример "отверстие в волнорезе" (см. рис. 7-8). Только на сей раз вообразим волнорез с двумя маленькими зазорами, расположенными неподалеку друг от друга. Плоские волны, ударяющиеся об волнорез, создадут в этом случае два синхронизированных (когерентных) источника круглой ряби. Волны от этих источников наложатся [58] друг на друга, как и показано на рис. 7-10.
В точке берега, которая лежит строго напротив центра перемычки, разделяющей зазоры, гребень одной волны всегда встречается с гребнем другой, потому что эта точка равноудалена от 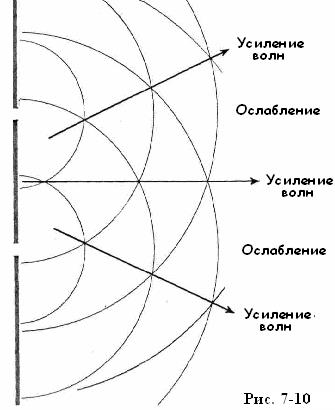 обоих зазоров волнореза. Волны от каждого зазора прибывают в эту точку одновременно, и интерференция здесь носит конструктивный характер — образуется волна удвоенной амплитуды (высоты), то есть наблюдается интерференционный максимум. Если мы сдвинемся вдоль берега от этой точки, то синхронизация волн будет нарушена, поскольку мы будем находиться ближе к одному зазору, чем к другому. Двигаясь вдоль берега, мы неизбежно попадем в точку, где гребни волн от одного зазора встречаются со впадинами в волнах от другого. Здесь интерференцияносит деконструктивный (разрушительный ) характер — результирующие волны получаются небольшими или отсутствуют вообще, то есть наблюдается интерференционный минимум. Двигаясь в том же направлении, мы достигнем точки, где волна от более близкого промежутка встречает предыдущую волну от более далекого. Здесь снова интерференция конструктивна, и волны снова высоки. Если мы продолжим движение по берегу, то снова достигнем точки деконструктивной интерференции, и так далее. Правило очень простое: если разница расстояний от источников волн до точки наблюдения составляет целое число длин волн, то интерференция конструктивна. Если же эта разница равна полуцелому (т.е. 1/2,3/2, 5/2, 7/2 и т. д.) числу длин волн, то интерференция деконструктивна.
обоих зазоров волнореза. Волны от каждого зазора прибывают в эту точку одновременно, и интерференция здесь носит конструктивный характер — образуется волна удвоенной амплитуды (высоты), то есть наблюдается интерференционный максимум. Если мы сдвинемся вдоль берега от этой точки, то синхронизация волн будет нарушена, поскольку мы будем находиться ближе к одному зазору, чем к другому. Двигаясь вдоль берега, мы неизбежно попадем в точку, где гребни волн от одного зазора встречаются со впадинами в волнах от другого. Здесь интерференцияносит деконструктивный (разрушительный ) характер — результирующие волны получаются небольшими или отсутствуют вообще, то есть наблюдается интерференционный минимум. Двигаясь в том же направлении, мы достигнем точки, где волна от более близкого промежутка встречает предыдущую волну от более далекого. Здесь снова интерференция конструктивна, и волны снова высоки. Если мы продолжим движение по берегу, то снова достигнем точки деконструктивной интерференции, и так далее. Правило очень простое: если разница расстояний от источников волн до точки наблюдения составляет целое число длин волн, то интерференция конструктивна. Если же эта разница равна полуцелому (т.е. 1/2,3/2, 5/2, 7/2 и т. д.) числу длин волн, то интерференция деконструктивна.
Вернемся теперь к опыту Юнга: заменим волнорез непрозрачным экраном, а зазоры в нем — узкими разрезами (щелями) в нем. На листе бумаги[59], расположенном достаточно далеко от щелей, можно будет увидеть картину чередующихся ярких и темных полос, параллельных щелям [60] (см. рис. 7-11). Самая яркая полоса  находится в центре картины и с каждой стороны её ограничивают темные полосы. Если измерить расстояние между полосами, то несложные геометрии-ческие расчеты позволят вычислить длину световой волны. Величина оказывается фантастически малой!: длины световых волн лежат в диапазоне от 0.00007 см (красный свет) до 0.00004 см (синий свет)[61]. Чтобы наблюдать интерференционную картину щели в непрозрачном экране должны быть очень узкими и очень близкими друг к другу, а экран для наблюдения должен быть расположен далеко от разрезов[62].
находится в центре картины и с каждой стороны её ограничивают темные полосы. Если измерить расстояние между полосами, то несложные геометрии-ческие расчеты позволят вычислить длину световой волны. Величина оказывается фантастически малой!: длины световых волн лежат в диапазоне от 0.00007 см (красный свет) до 0.00004 см (синий свет)[61]. Чтобы наблюдать интерференционную картину щели в непрозрачном экране должны быть очень узкими и очень близкими друг к другу, а экран для наблюдения должен быть расположен далеко от разрезов[62].






