Работа и кинетическая энергия

Расширяя ньютоновский язык описания движения, мы вводим новую меру движения, называемую кинетической энергией (KE), которая определяется формулой:

(5.1)

Как мы скоро увидим, множитель в формуле (5.1) появляется, подобно тому, как и в формуле Галилея для равноускоренного движения.

Определение кинетической энергии выглядит обманчиво похожим на определение импульса, но факт, что в нем скорость возводится в квадрат, имеет решающее значение. Именно это делает кинетическую энергию ненаправленной (скалярной) мерой движения. Положительна ли скорость или отрицательна, ее квадрат всегда положителен. Движения в противоположных направлениях не уравновешиваются!

Второй шаг определяет величину, называемую работой. Работа — мера изменения энергии под действием силы. Работа вычисляется перемножением силы F и расстояния, s, на котором тело движется строго в направлении действия силы. Например: если сила — сила тяжести, то мы учитываем только вертикальное перемещение движущего тела. Это определение работы наиболее просто выражается математической формулой, содержащей тригонометрическую функцию косинус.

(5-2)

где — угол между силой и направлением движения.

Даже если Вы не очень дружите с тригонометрией, смысл формулы (5-2) легко объяснить. Если сила направлена вперёд, то меньше чем 90°. Для таких углов косинус положителен. Для углов от 90° до 180° косинус отрицателен. Для угла 90° косинус равен нулю, и, таким образом, никакая работа не совершается. А ведь это именно то, что мы потребовали в п. 2 предыдущего раздела!

Чтобы проиллюстрировать использование понятий работы и кинетической энергии, рассмотрим тело, которое начинает двигаться из состояния покоя под действием постоянной силы. Оно может двигаться только в направлении силы, так что угол =0°, а его косинус равен единице. Таким образом, работа — это просто .

Движение тела происходит с постоянным ускорением, так что складывается точно такая же ситуация, что описана в Главе1. Значит, можно использовать формулу 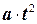для вычисления перемещения. Мы также можем использовать второй закон Ньютона и заменить силу произведением . Тогда мы имеем:

Этот пример, адресованный тем, кто не боится математики, показывает, что совершенная силой работа равна появившейся у тела кинетической энергии.

Рассмотрим теперь автомобиль, движущийся с постоянной скоростью. В этом случае сила, производимая двигателем, тоже совершает работу, но эта работа не приводит к увеличению кинетической энергии. Дело в том, что сила, производимая двигателем, уравновешена трением и сопротивлением воздуха. Работа, совершенная этой силой, однако, не теряется — она переходит в другие формы энергии. А это как раз именно то, что мы зафиксировали в п. 3 предыдущего раздела!

Можем ли мы вернуть свои деньги?

Все те преобразования энергии, которые мы успели рассмотреть, были сопряжены с существенными изменениями в окружающем мире: сгорает бензин, нагреваются тормоза и т.д. Однако с некоторыми силами, и особенно с силой тяжести, происходит что-то таинственное. Падающий камень приобретает энергию, при своем падении. Откуда эта энергия? Ведь ничего, кроме местоположения камня не меняется!

Ответ на этот вопрос помогает найти пример, показанный на рис. 5 - 1. С точки зрения энергии — это свободное падение “наоборот”, поскольку при подъёме камня с помощью лебёдки энергия расходуется без какого-либо видимого результата, кроме изменения в положении камня.

Снова, с ньютоновской точки зрения ничего интересного здесь не происходит.
На большей части своего пути “вверх” камень движется с постоянной скоростью — его вес, точно уравновешен силой натяжения веревки. Правда, для того, чтобы привести камень в движение должен существовать краткий момент, когда сила натяжения верёвки превышает вес камня, но после этого движение камня равномерно. В терминах законов Ньютона это означает, что камень может и вообще остановиться. А вот с точки зрения человека, работающего за лебёдкой, различие есть, и весьма значительное. Да, он может остановить подъём груза, поставить лебёдку на тормоз и уйти. Но это не поднимет камень — для дальнейшего подъёма придется ещё попотеть, развивая мышечные усилия и совершая работу. Эта работа — произведение веса mg на расстояние h — не идет на увеличение кинетической энергии камня. Так что же, эта работа потеряна навсегда?

Ответ: конечно же, нет! Если перерезать веревку, то камень начнет падать. Сила тяжести действует на камень, и он достигнет поверхности земли с кинетической энергией, равной работе силы тяжести. Таким образом, камень будет двигаться с такой же скоростью, которую он приобрел бы, если бы затраченная работа была совершена над ним в отсутствии силы тяжести.

Энергию, "запасенную" таким образом называют потенциальной энергией. Смысл слова очевиден. Поднимая камень, мы создали ситуацию, которая потенциально может создать движение. Перерезав верёвку, мы преобразуем этот потенциал в реальное движение.

Процесс преобразования потенциальной энергии в кинетическую энергию является постепенным. Когда камень проделал только одну десятую часть своего пути к земле, то сила тяжести совершила только одну десятую часть своей работы. Одна десятая часть энергии стала кинетической, другие девять десятых частей остаются потенциальными. Поскольку камень продолжает свое падение, потенциальная энергия постепенно расходуется, а кинетическая — увеличивается. Когда камень достигнет земли, вся потенциальная энергия будет преобразована в кинетическую, и работа, затраченная на подъем камня, проявит себя как кинетическая энергия камня.

Эти отношения могут быть выражены математически в форме

(5-4)

где h — высота на которой находится падающий камень, а Н — высота, с которой он начал своё падение. С помощью этой формулы для любой высоты h мы можем вычислить скорость камня, поскольку его кинетическая энергия — это разность между mgH и mgh.

Но ведь Галилей делал то же самое, не пользуясь понятиями кинетической и потенциальной энергии.

Да, действительно, если бы уравнение (5-4) было применимо только к падающему камню, то его вряд ли стоило бы даже записывать. Но рассмотрим аттракцион, схематически изображенный на рис. 5 - 2 [5]. Формула (5-4) применима и в этой ситуации. Как только тележка поднята на вершину первого возвышения и отпущена, она движется под действием только двух сил: силы тяжести и силы реакции рельс. Однако последняя всегда перпендикулярна движению, и, следовательно, не совершает никакой работы. Скорость, которую приобретает тележка в разных точках этого извилистого рельефа, зависит только от высоты этой точки над основанием и совпадает со скоростью тела, свободно падающего с высоты Н[6].

 

Энергия и атомы

Одним из самых больших достижений физики XIX столетия было осознание того, что, если рассматривать материю как вещество, состоящее из атомов, то все законы термодинамики могут быть поняты, исходя из того, что теплота — это ничто иное, как энергия движущихся атомов.

Вообразим (см. рис. 5 - 3), столкновение двух пластилиновых шаров одинаковой массы, движущихся навстречу друг к другу с одинаковыми скоростями. После столкновения они слипнутся и остановятся. Если не рассматривать внутреннюю структуру шаров, то мы видим, что полный импульс системы сохраняется, а вот энергия движения теряется! Заметим, что в механике закон сохранения импульса, независимо от того уровня, на котором рассматривается система, выполняется без всяких ограничений. Если же мы будем исследовать вещи на более глубоком уровне, то обнаружим, что энергия движения шаров перешла в движение атомов, из которых состоят пластилиновые шары. Это может быть замечено по увеличению температуры шаров, поскольку температура – это ни что иное как мера средней кинетической энергии (это будет показано в Главе13). Движение атомов является сложным, хаотическим и случайным. Нет никакого способа полностью обратить процесс столкновения, то есть заставить все атомы пластилинового шара двигаться в одном направлении, и, тем самым, восстановить первоначальную энергию шара.

Если мы переходим из макроскопического мира шаров к микроскопическому миру их атомов, то закон сохранения энергии сохраняет в некоторой степени свой механический характер. Так, например, химическая энергия может рассматриваться как потенциальная энергия тех сил, которые связывают атомы вещества воедино. Это вело к надежде, что все природные явления, если разобраться в их микроскопических деталях, допускают механическую интерпретацию. Единственными истинными формами энергии в этом случае оказались бы кинетическая и потенциальная.

Рассмотренный пример столкновения пластилиновых шаров демонстрирует и другое преимущество концепции “энергия”. С точки зрения одного только закона сохранения импульса нет никакого различия между шарами до и после столкновения, или же между упругим соударением и неупругим. Закон сохранения энергии, однако, позволяет сделать такое различие, так как энергия — это мера движения, не зависящая от направления движения. Действительно, законы упругого соударения получены из предположения, что одновременно выполняются законы сохранения и импульса и энергии. Совместное применение этих законов позволяет дать более полное описание движения объектов.

Можно теперь более подробно проанализировать примеры столкновений, рассмотренных в Главе 2. с точки зрения закона сохранения энергии. В первом примере, где шары слипаются, часть кинетической энергии идёт на повышение температуры. При упругом соударении кинетическая энергия сохраняется неизменной. Третий пример показывает, что существенное количество энергии было преобразовано в кинетическую форму в момент столкновения. (Возможно к одному из шаров был прикреплен взрывчатый патрон!)

Звёзды, планеты и жизнь

Если введенное выше понятие потенциальной энергии, которая всегда оказывается отрицательной, кажется Вам “неэстетичным”, то обратите внимание, что именно знак “минус” отражает процесс создания связанной пары объектов. Если мы попытаемся “построить” Cолнечную систему, состоящую из Земли и Солнца, находящихся на отдаленном расстоянии от друг друга, то для того чтобы поместить Землю на её жёстко определённую орбиту, мы должны “вынуть” энергию из системы. В противном случае Земля свободно возвратилась бы к своему удаленному от Солнца местоположению. Вполне разумно рассматривать объекты, настолько удаленные друг от друга, что они не проявляют никаких сил взаимодействия, как обладающие нулевой энергией. Если энергия “вынута”, чтобы связать объекты, то вполне разумно рассматривать это как наличие отрицательной энергии. Когда мы приступим к изучению теории относительности, то мы увидим, что эта отрицательная энергия имеет вполне конкретное проявление — дефект массы.

Этот подход является основанием для весьма популярной теории того, как были сформированы звезды и планетарные системы. Всё начиналось с огромного, разбросанного облака прохладного газа. Облако сжималось к своему центру под действием гравитации, потенциальная энергия при этом преобразовывалось в движение молекул, то есть в теплоту. В некоторых точках температура становилась настолько высокой, что зажигались термоядерные реакции. Так рождались звёзды.

Что касается образования планет, то предположим, что облако изначально очень медленно вращается. На больших расстояниях скорости этого вращения очень маленькие, но при сжатии облака, скорости увеличиваются — подобно тому как увеличивается скорость вращения танцовщика или фигуриста, когда он прижимает к корпусу ранее вытянутые в стороны руки. К тому времени, когда облако достигает сравнительно небольших размеров звезды, его вращение может оказаться слишком быстрым для того, чтобы позволить дальнейшее сжатие. Часть облака отрывается[7], и никогда не достигнет его центра. В результате “брызги” превращаются в объекты, у которого слишком мало потенциальной энергии для того, чтобы достигнуть термоядерных температур. Так формируются прохладные планеты. Тот факт, что все планеты Солнечной системы, да и само Солнце, вращаются в одном и том же направлении, подтверждает эти рассуждения.

Даже после того, как человечество достойно приняло удар по своей гордости, признав, что Земля не является центром Вселенной, возникла надежда, что Солнечная система является уникальным результатом некоторого катастрофического космического происшествия. Но всё же сегодня кажется намного более вероятным, что планеты — это правило, а не исключение. Среди бесчисленных звезд и галактик звезд, должны быть многочисленные планеты столь же гостеприимные к жизни, как наша. Было бы глупо предполагать, что жизнь ограничена нашим уголком Вселенной и что тайна сознания дана нам одним.