Луна как связь земного и небесного.

 

Однако законы Кеплера говорят только об относительных скоростях движения разных планет, или о скоростях одной планеты в разных точках её орбиты. Не зная ни величины силы, действующей на планету, ни массы Солнца, ни коэффициента γ в формуле 4-1, не было возможности завершить анализ: Ньютон продемонстрировал, что его закон может объяснить, почему год на Марсе вдвое длиннее года на Земле, но длину самого года вычислить не мог. Так что простое объяснение законов Кеплера не могло разрушить дихотомию (раздвоение) между явлениями земными и небесными.

К счастью для Ньютона, наша Земля имеет спутник, Луну. Так как одна и та же Земля создаёт ускорение свободного падения камня и ускорение Луны на её орбите, то единственное отличие этих двух явлений состоит в том, что Луна находится много дальше от центра Земли, и поэтому изменение силы гравитации можно подсчитать. По измеренному ускорению камня на поверхности Земли можно рассчитать, какое ускорение должна иметь на своей орбите Луна, если она подвержена действию только силы гравитации Земли. Будет ли соответствовать этот расчёт наблюдаемому движению Луны? Здесь для Ньютона открывалась возможность прямого количественного доказательства того, что одна и та же сила вызывает движения и камня, и Луны.

Уже во времена Ньютона расстояние до Луны было известно, т.к. его довольно легко измерить. Оно составляет 380000 км, что в 60 раз больше радиуса Земли. Таким образом, ускорение под действием силы гравитации Земли на лунной орбите должно быть в (60)² раз меньше, чем ускорение свободного падения на Земле, то есть:

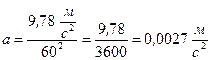
Если мы примем, что движение Луны является движением материального объекта под действием одной только силы земного тяготения, то «а» должно быть ускорением на её орбите.

Остаётся подсчитать наблюдаемое ускорение Луны, используя формулу, полученную в предыдущей главе. Скорость Луны на её орбите равна 1016 мс^-1. Она получена делением длины орбиты 2π·380000 км на длину лунного месяца 27,32 дня. Таким образом, искомое ускорение получается

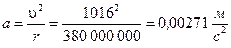
Учитывая тот факт, что орбита Луны не совсем круговая, а слабо эллиптическая, соответствие двух величин ускорения «а» является просто великолепным.

Чтобы убедиться, что мы не потеряли нить рассуждений, занимаясь арифметикой, резюмируем сказанное. Итак, мы начали с предположения, что Луна, являясь материальным объектом, подчиняется тем же законам, которые действуют на Земле. Мы обнаружили, что ускорение Луны меньше ускорения свободного падения тела на Земле ровно во столько раз, во сколько отличаются квадраты их расстояний от центра Земли.

Этот результат был шокирующим. Конечно, один такой результат может оказаться простым совпадением, и окончательное доказательство ещё впереди и потребует более детальных расчётов других явлений. И всё же приведённый расчёт был прочной связью и количественной корреляцией между явлением на Земле и явлением на небесах.

Но самый главный аспект теории оставался не доказанным: её претензия на открытие универсальной силы, которая действует между любыми телами на любом расстоянии и пропорциональна произведению их масс. По законам Кеплера можно было убедиться, что сила притяжения Солнца, обратно пропорциональная квадрату расстояния, объясняет движение всех планет Солнечной системы (включая Землю). Подобная сила, создаваемая Землёй, объясняет движение всех падающих тел и движение Луны вокруг Земли. Однако, не зная масс Солнца и Земли, Ньютон имел слабые основания для утверждения, что сила пропорциональна массе большего «центрального» объекта в каждом из упомянутых случаев. И он не имел никаких оснований утверждать, что эта сила может действовать и, например, между двумя камнями на Земле, разве что мог утверждать, что земные камни взаимодействуют слишком слабо, чтобы это можно было измерить. Тем не менее, достижения теории тяготения были столь убедительны, и они так хорошо соответствовали духу ньютоновской физики, что немногие физики серьёзно сомневались в универсальности теории с момента её публикации. Универсальность теории тяготения не имела прямого подтверждения, пока полтора столетия спустя Генри Кавендиш не изобрёл прибор для измерения слабого взаимодействия двух тел в лаборатории. Вера в закон гравитации Ньютона была столь велика, что Кавендиш назвал свой эксперимент не «подтверждением закона Всемирного тяготения», а «взвешиванием Земли»; это название также опиралось на недоказанное утверждение, что сила земного тяготения, действующая на камень, пропорциональна массе Земли, также как и массе камня. Так как он измерил силу между двумя объектами известных масс, Кавендиш впервые получил в свои руки всю информацию, необходимую для вычисления гравитационной постоянной γ в формуле Ньютона. Как только эта константа стала известной, вес известной массы (конкретного тела) на Земле можно было использовать для расчета массы Земли, так как все остальные члены в формуле для силы известны.

По крайней мере в течение столетия после публикации «Принципов», самым важным приложением и подтверждением ньютоновских законов механики и гравитации оставались расчеты движений планет. И только в XIX веке, когда создание машин перестало, наконец, быть процессом проб и ошибок, ньютоновские законы движения получили своё практическое применение.

 

Гипотез не изобретаю.

 

Если теория гравитации была величайшим достижением Ньютона, то одна её особенность должна была представлять для него самые серьёзные затруднения. Это было понятие о действии на расстоянии, согласно которому два тела на большом расстоянии друг от друга могли взаимодействовать без всякого посредника, кроме пустого пространства между ними. Неофициально, Ньютон отвергал подобную идею, как абсурдную, и был уверен, что должна существовать материальная субстанция, способная передавать силу. Хотя при этом он не имел никакого конкретного представления о том, что бы это могло быть. Но его публичные заявления были совершенно иными. Из-за почти параноидального отвращения к научным дебатам он отказался участвовать в диспуте, надменно заявив: «Нypothesis non fingo!», что в переводе означает «Гипотез не изобретаю!».

Позиция Ньютона в этом вопросе была крайне неудачной для последующего развития физики. В то время она оставляла теорию уязвимой для атак со стороны сторонников Декарта, которые почувствовали в ней «запах серы», т.е. способ оккультного объяснения природы, которое предполагалось изгнать из науки навсегда.

К сожалению, последствия оказались худшими, чем сама атака. Когда следующие поколения физиков разрешили проблему в пользу Ньютона, вера в чистое действие на расстоянии стала высшим тестом рациональности. И когда в XIX веке появилась, как блестящая идея, концепция поля, она встретила очень сильное сопротивление сторонников предрассудка дальнодействия. Поля в нашей книге появятся в 6 главе и будут главной темой, так как сегодня посредник взаимодействия, которым Ньютон так бесцеремонно и надменно пренебрёг, считается таким же реальным, как сама материя.

Математическая форма закона гравитации напрашивается на простую интерпретацию. Закон обратной пропорциональности квадрату расстояния имеет силу для любого «влияния», которое распространяется одинаково по всем направлениям от центрального источника, как свет от «голой» лампочки: чем дальше от источника, тем больше общая площадь, на которую распространяется свет. Общая площадь возрастает как квадрат расстояния, поэтому доля света, который падает на любую заданную площадь, такую, например, как лист бумаги, должна уменьшаться точно в такой же степени. Если гравитация тоже нечто такое, что распространяется подобным образом, едва ли нужно искать что-то другое, чем закон обратной пропорциональности квадрату расстояния.

Именно такой ход рассуждений привёл Гука и Галлея к догадке, что гравитация может подчиняться закону квадратичной обратной пропорциональности, ещё до того, как Ньютон решил этот вопрос, доказав, что он ведёт к законам Кеплера. Имей Ньютон бóльшую выдержку в публичных диспутах, или если бы он стал менее культовым героем, эта хорошая идея не была бы отодвинута на полтора века.

 

Глава 5. Романс энергии

Храни нас Бог
От виденья, единого для всех,
И снов Ньютона.

Уильям Блейк

.

Непрерывный триумф физики Ньютона и астрономии продолжался целое столетие после публикации “ Принципов..”. Математические вычисления превратились в аналитический инструмент, и движения Луны и планет были рассчитаны с удивительной точностью[2]. Однако к концу этого периода многие ученые стали понимать, что с практической точки зрения законы Ньютона, да и само понятие импульса являются только началом науки о движении, динамики, а не её завершением, как это казалось вначале.

Проблема заключалась том, что механика Ньютона рассматривала силу как основное (базовое) понятие, и развивалась от этой отправной точки. Она не давала готового ответа на вопрос, с которым пионеры промышленной революции сталкивались ежедневно: “Что нужно сделать, чтобы произвести силу?” Инженеры и изобретатели стремились создать движение там, где его ранее не существовало. Всё, что мог предложить им Ньютон — это гарантия того, что если им удастся сделать это, то при этом неизбежно возникнет равное и противоположное движение. Это была помощь, но не очень существенная.

Поэты и философы, которые несколько десятилетий назад восторженно приветствовали освобождающее влияние идей Ньютона, вдруг стали говорить и об их “темной” стороне. Действительно, холодный аналитический метод, ищущий максимальную точность во всём, часто терял из виду красоту и единство природы. Они восторгались мощью человеческого духа и боялись бесплодного рационализма, который, как им казалось, не оставлял места для эмоциональной творческой мысли.

Реакцией физики на эти критические замечания, исходящие из двух противоположных полюсов, стало развитие понятия энергия. Сегодня это понятие не только занимает центральное место в физической теории, но и связывает физику с другими науками и с реальным миром.

Чем мы “платим” за силу?

Несколько примеров помогут нам показать практические недостатки строгой ньютоновской физики и укажут путь к новым понятиям, которые сделают её более полезной.

Рассмотрим сначала пулю, выпущенную из ружья. Закон сохранения импульса требует, чтобы оружие отскочило с тем же (но противоположно направленным!) импульсом, что и у пули. Общий импульс был равен нулю до выстрела и остается таковым и после выстрела. Но простой здравый смысл говорит нам, что кое-что существенное изменилось. Кое-что было вынуто из небольшого количества пороха и преобразовано в движение пули и оружия. При выстреле порох был преобразован и потерял способность сделать это снова. Итак, физика должна быть в состоянии делать различие между ситуациями “ до ” и “ после ”.

Теперь рассмотрим пример одного из самых знакомых практических применений силы — еёспособность передвигать транспортные средства, например, автомобиль. Большую часть времени автомобиль движется с довольно постоянной скоростью, но все же некоторая сила необходима для того, чтобы преодолевать трение и сопротивление воздуха. С точки зрения законов Ньютона это абсолютно понятный и полностью неинтересный случай. Движущая автомобиль сила точно уравновешивает сопротивление, так что результирующая сила, а вместе с ней и ускорение равны нулю.

Законы Ньютона не полностью бесполезны в этой ситуации. Они говорят проектировщику, какая дополнительная сила необходима, чтобы ускорить автомобиль и какую силу должны проявить тормоза, чтобы при необходимости остановить машину.

Мы, однако, прекрасно понимаем, что двигатель жжет топливо, а тормоза — нет. Тормоза, тем не менее, при торможении нагреваются, и конструкторы должны искать способы избавиться от этой теплоты. (Вопросы о том, сколько топлива должен потреблять двигатель и до какой температуры могут быть нагреты тормозные колодки, явно лежат за пределами динамики.)

Когда же автомобиль движется по кривой с постоянной скоростью, ситуация иная. При малом радиусе поворота ускорение автомобиля почти такое же, как при его быстром старте (“педаль газа в пол”), но при этом нет существенного увеличения расхода топлива.

Чтобы разогнать автомобиль, мы должны взять кое-что от топлива; чтобы остановить его, мы повышаем температуру тормозов; а вот чтобы изменить направление его движения ничего не нужно брать или отдавать внешнему миру. Однако в каждом из этих случаев действуют силы примерно одной и той же величины. Направление силы — вот что имеет значение! За силу, направленную вперёд, нужно заплатить (на бензоколонке), за силу, направленную назад придется платить в автомастерской (при замене тормозных колодок), а вот сила, перпендикулярная движению ничего не стоит![3]

Используя эти примеры мы можем составить программу дальнейшего развития динамики:.

1. Необходим новый закон сохранения, имеющий дело с ненаправленной (скалярной [4]) мерой движения, которая, в отличие от импульса, не обнуляется при сложении двух противоположных движений.

2. При введении этой меры движения в ньютоновскую физику всё же нужно учитывать направление силы относительно движения: сила, направленная вперёд должна давать положительный эффект, направленная назад — отрицательный, а сила, перпендикулярная движению — никакого эффекта вообще.

3. И, наконец, мы должны найти связь этой меры движения с вещами, которые, на первый взгляд, не имеют никакого отношения к движению: теплота и то кое-что, что скрывается в топливе и взрывчатых веществах.

Пришло, наконец, время дать название этой мере, которая иногда проявляет себя как движение, а иногда и в других формах; Это таинственное кое-что называют энергией. Термин был заимствован физикой от поэтов и философов, которые сожалели о его бесплодии. Мы начнем исследование энергии с поиска её места в ньютоновской физике.