Допустим, имеется часть электрической схемы, представленная на рисунке 2.94, в которой выделены узлы 1, 2, 3 и 4.
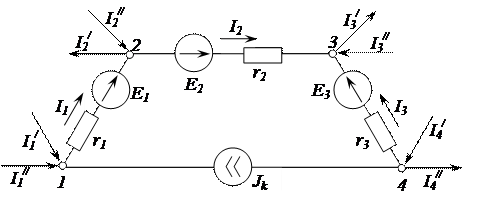
Рисунок 2.94 – Электрическая цепь
Между узлами 1 и 4 включен источник тока. Необходимо избавиться от ветви с источником тока с целью уменьшения количества ветвей. Преобразования должны быть эквивалентными, т.е. с сохранением основных энергетических соотношений (например, баланс мощности, законы Кирхгофа).
На первом этапе источник тока разобьем на три источника тока, подсоединенных между 1 и 2, 2 и 3, 3 и 4 узлами (рис. 2.95).

Рисунок 2.95 – Эквивалентная электрическая цепь после переноса
источника тока
Эти измененния касаются 2 и 3 узла. Они эквивалентны, т.к. к каждому узлу мы подсоединили по две ветви с источниками тока  . По первому закону Кирхгофа соотношения выполняются, второй закон Кирхгофа мы не изменяли.
. По первому закону Кирхгофа соотношения выполняются, второй закон Кирхгофа мы не изменяли.
На следующем этапе параллельно подсоединенные источники тока, заменяем источниками напряжения: 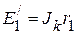 ,
, 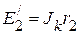 ,
,  .
.
В результате электрическая схема, приведенная на рисунке 2.74, уменьшится на одну ветвь (рис. 2.96).
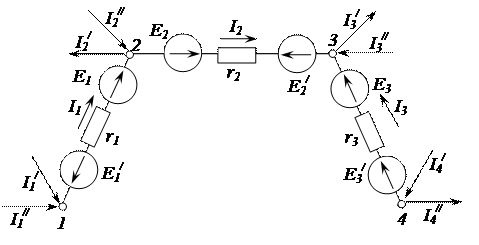
Рисунок 2.96 – Эквивалентная электрическая цепь
Пример 2.25. Рассмотрим преобразование электрических цепей, в которых источник тока охватывает несколько ветвей, на примере электрической цепи, рассматриваемой в примере 2.3 и приведенной рисунке 2.97, параметры которой Jk3 = 3 А, Е2 = 50 В, Е5 = 60 В, r1 = 6 Ом, r2 = 10 Ом, r4 = 8 Ом, r5 = 10 Ом, r6 = 5 Ом.

Рисунок 2.97 – Электрическая цепь постоянного тока
1. Осуществляем предварительный анализ схемы.
Количество ветвей –  , количество узлов –
, количество узлов – 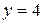 .
.
2. Применяем преобразование электрических цепей, в которых источник тока охватывает несколько ветвей. В результате схема приобретает вид, представленный на рисунке 2.98.
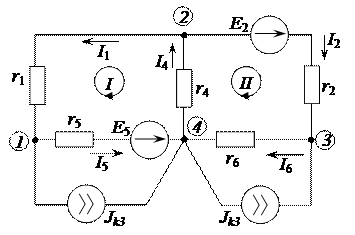
Рисунок 2.98 – Эквивалентная электрическая цепь постоянного тока
3. Параллельно подсоединенные источники тока, заменяем источниками напряжения 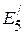 и
и 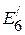 , которые соответственно равны:
, которые соответственно равны:
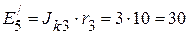 В,
В,
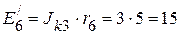 В.
В.
В результате схема приобретает вид, представленный на рисунке 2.99.
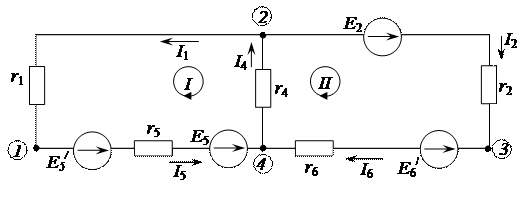
Рисунок 2.99 – Эквивалентная электрическая цепь постоянного тока
В результате электрическая схема, приведенная на рисунке 2.99, уменьшилась на три ветви и два узла.
4. Применяя свойства последовательного соединение резистивных элементов и последовательного соединение ЭДС, для электрической цепи, изображенной на рисунке 2.99, получим эквивалентную электрическую цепь постоянного тока, представленную на рисунке 2.100.

Рисунок 2.100 – Эквивалентная электрическая цепь постоянного тока
На приведенной схеме,
 Ом,
Ом,
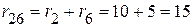 Ом,
Ом,
 В,
В,
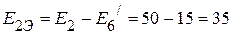 В.
В.
5. Рассчитываем токи в эквивалентной электрической цепи постоянного тока.
5.1. Осуществляем предварительный анализ схемы.
Количество ветвей – 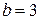 , количество узлов –
, количество узлов – 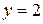 .
.
5.2. Рассчитываем токи в ветвях методом узловых потенциалов.
Потенциал четвертого узла принимаем равным нулю:  . Следовательно, необходимо определить потенциал
. Следовательно, необходимо определить потенциал  .
.
5.2.1. Составляем уравнение для определения потенциала  :
:
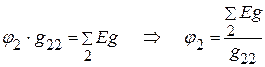 .
.
5.2.1.1. Подставляем числовые значения и находим потенциал 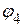 .
.
5.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
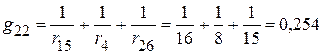 См;
См;
Узловые токи
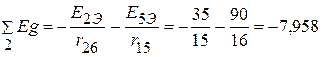 А.
А.
5.2.1.3. После подстановки цифровых значений, определяем потенциал  :
: 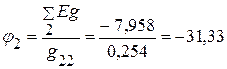 В.
В.
5.2.2. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.100.
 А,
А,
 А,
А,
 А.
А.
5.2.3. Используя второй закон Кирхгофа, определяем токи 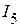 и
и  в электрической цепи, приведенной на рисунке 2.99.
в электрической цепи, приведенной на рисунке 2.99.
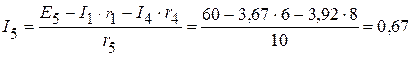 А;
А;
 А.
А.
Токи в ветвях, рассчитанные в примерах 2.3 и 2.25 совпадают.






