Соединение, представленное на рисунке 2.109 а, называют трехлучевой звездой, а на рис. 2.109 б – треугольник сопротивлений.
Ставится задача осуществить преобразование звезды сопротивлений в эквивалентный треугольник и наоборот.
В общем случае звезда (треугольник) сопротивлений подключены к разветвленной схеме в узлах 1, 2, 3. Преобразования должны быть эквивалентными, т.е. в результате преобразований в остальной части схемы никаких изменений нет. Токи  ,
,  ,
,  и потенциалы
и потенциалы  ,
,  ,
,  остаются неизменными.
остаются неизменными.

Рисунок 2.109 – Трехлучевая звезда и треугольник сопротивлений
Для доказательства рассмотрим преобразования треугольника сопротивлений (рис. 2.109 б) в эквивалентную звезду схему треугольник (рис. 2.109 а). В этом случае исходными данными являются величины сопротивлений треугольника  ,
,  ,
,  . Необходимо определить величины сопротивлений эквивалентной звезды –
. Необходимо определить величины сопротивлений эквивалентной звезды –  ,
,  ,
,  .
.
Из схемы треугольник (рис. 2.109 б), согласно второго закона Кирхгофа, имеем:

Используя первый закон Кирхгофа для 1 и 2 узлов, соответственно получим:
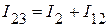 ,
,  .
.
Подставим полученные выражения, в уравнение, составленное по второму закона Кирхгофа. В результате имеем:
 , откуда
, откуда
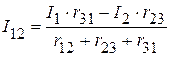 .
.
Тогда напряжение  между узлами 1 и 2:
между узлами 1 и 2:

 .
.
Рассмотрим схему звезда (рис. 2.109 а). Для данной схемы
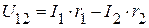 .
.
Сравнивая полученные выражения для U 12,
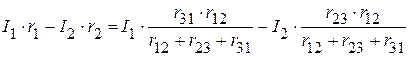 .
.
Так как схемы эквивалентные то напряжение одинаково и коэффициенты при токах  и
и  тоже должны быть одинаковыми. Следовательно:
тоже должны быть одинаковыми. Следовательно:
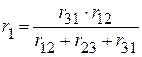 ,
,  ,
, 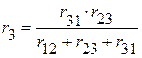 .
.
Пример 2.27. Рассмотрим эффективность преобразование треугольника сопротивлений в звезду сопротивлений.
1. Исходная схема (рис. 2.110 а) содержит  ветвей и
ветвей и  узла.
узла.
2. Преобразовываем треугольник сопротивлений  ,
,  ,
,  в эквивалентную звезду
в эквивалентную звезду  ,
,  ,
,  , сопротивления которой соответственно равны:
, сопротивления которой соответственно равны:
 ,
, 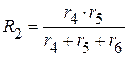 ,
,  .
.
В результате преобразования получим эквивалентную схему, представленную на рисунке 2.110 б.

Рисунок 2.110 – Преобразование треугольника сопротивлений
в эквивалентную звезду
Таким образом, после преобразования произошло упрощение схемы: вместо шести ветвей в первой схеме получили три ветви во второй; вместо четырех узлов в первой схеме получили два узла во второй.
Пример 2.28. Рассмотрим пример взаимных преобразований треугольник–звезда на конкретном примере. В схеме, приведенной на рисунке 2.111, заданы напряжения источников ЭДС Е1 = 20 В, Е3 = 15 В и значения сопротивлений r 1 = 150 Ом, r 2 = 50 Ом, r 3 = 75 Ом, r 4 = 1000 Ом, r 5 = 800 Ом, r 6 = 200 Ом. Определить токи ветвей.

Рисунок 2.111 – Исходная электрическая цепь постоянного тока
1. Исходная схема (рис. 2.111) содержит  ветвей и
ветвей и  узла.
узла.
2. Преобразовываем треугольник сопротивлений  ,
,  ,
,  в эквивалентную звезду
в эквивалентную звезду  ,
,  ,
,  , сопротивления которой соответственно равны:
, сопротивления которой соответственно равны:
 Ом,
Ом,
 Ом,
Ом,
 Ом.
Ом.
В результате преобразования получим эквивалентную схему, представленную на рисунке 2.112.

Рисунок 2.112 – Преобразование треугольника сопротивлений
в эквивалентную звезду
Таким образом, после преобразования произошло упрощение схемы: вместо шести ветвей в исходной схеме получили три ветви в преобразованной схеме; вместо четырех узлов в исходной схеме получили два узла в преобразованной схеме.
3. Рассчитываем токи в электрической схеме, приведенной на рисунке 2.112, методом узловых потенциалов.
3.1. Осуществляем предварительный анализ схемы.
Количество ветвей – 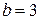 , количество узлов –
, количество узлов – 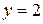 .
.
3.2. Рассчитываем токи в ветвях методом узловых потенциалов.
Потенциал четвертого узла принимаем равным нулю:  . Следовательно, необходимо определить потенциал пятого узла
. Следовательно, необходимо определить потенциал пятого узла  .
.
3.2.1. Составляем уравнение для определения потенциала  :
:
 .
.
5.2.1.1. Подставляем числовые значения и находим потенциал  .
.
5.2.1.2. Сумма проводимостей ветвей, подключенных к соответствующим узлам:
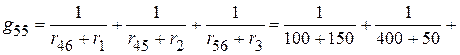
 См;
См;
Узловые токи
 мА.
мА.
5.2.1.3. После подстановки цифровых значений, определяем потенциал  :
:  В.
В.
5.2.2. Определяем токи в ветвях электрической цепи, приведенной на рисунке 2.112.
 мА,
мА,
 мА,
мА,
 мА.
мА.
3.2.5. Используя второй закон Кирхгофа, определяем токи  и
и  в электрической цепи, приведенной на рисунке 2.111:
в электрической цепи, приведенной на рисунке 2.111:
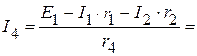
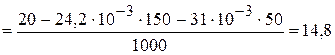 мА;
мА;

 мА.
мА.
3.2.6. Используя первый закон Кирхгофа, определяем ток  в электрической цепи, приведенной на рисунке 2.111:
в электрической цепи, приведенной на рисунке 2.111:
 мА.
мА.
4. Проверяем решение, составив баланс мощностей.
4.1. Мощность, генерируемая источниками питания:
 Вт,
Вт,
 Вт.
Вт.
Суммарная мощность источников:
 Вт.
Вт.
4.2. Мощность, потребляемая приемниками:
 Вт,
Вт,
 Вт,
Вт,
 Вт,
Вт,
 Вт,
Вт,
 Вт,
Вт,
 Вт.
Вт.
Суммарная мощность, потребляемая приемниками:


 Вт.
Вт.
4.3. Из сравнения генерируемой мощности источником и потребляемой мощности приемниками, следует, что погрешность вычислении  и не превышает 0,5%.
и не превышает 0,5%.
Возможно и обратное преобразование – звезды сопротивлений в эквивалентный треугольник (рис. 2.113).

Рисунок 2.113 – Треугольник сопротивлений и трехлучевая звезда
В этом случае исходными данными являются сопротивления  ,
,  ,
,  . Необходимо определить сопротивления
. Необходимо определить сопротивления  ,
,  ,
,  .
.
Рассмотрим схему звезда (рис. 2.113 б). Ток  равен:
равен:
 .
.
Из метода узловых потенциалов  .
.
Тогда ток
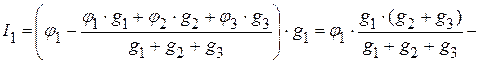
 .
.
Из схемы треугольник (рис. 2.113 а), имеем:  .
.
Ток  ,
,  .
.
Тогда ток
 .
.
Сравнивая ток  при соединении звездой и треугольником, и учитывая эквивалентность преобразований, имеем:
при соединении звездой и треугольником, и учитывая эквивалентность преобразований, имеем:
 ,
,  .
.
Аналогично  .
.
Если в вышеуказанные формулы вместо проводимостей 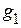 ,
, 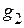 ,
,  ,
,  подставить величины сопротивлений
подставить величины сопротивлений  ,
,  ,
,  ,
,  , тогда
, тогда
 .
.
В общем виде формулы преобразования имеют вид:
 ;
;  ;
;  .
.
Пример 2.29. Рассмотрим пример взаимных преобразований звезда–треугольник на конкретном примере. В схеме, приведенной на рисунке 2.114 а, заданы ЭДС Е = 20 В и значения сопротивлений r 1 = 4 Ом, r 2 = 1 Ом, r 3 = 1 Ом, r 4 = 2 Ом, r 5 = 4 Ом, r 6 = 5 Ом. Определить токи ветвей.

Рисунок 2.114 – Электрическая схема
1. Расчет токов целесообразно осуществлять, преобразуя предварительно звезду  в треугольник по схеме, приведенной на рисунке 2.114 б. В соответствии с формулами преобразования звезды сопротивлений в треугольник
в треугольник по схеме, приведенной на рисунке 2.114 б. В соответствии с формулами преобразования звезды сопротивлений в треугольник
 Ом,
Ом,
 Ом,
Ом,
 Ом.
Ом.
2. Токи в ветви  определяем по закону Ома:
определяем по закону Ома:
 А.
А.
3. Ветви  ,
,  также как и ветви
также как и ветви 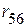 ,
,  соединены параллельно:
соединены параллельно:
 Ом,
Ом,
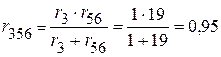 Ом.
Ом.
4. Ветви  и
и  соединены последовательно:
соединены последовательно:
 Ом.
Ом.
5. Общий ток:  А.
А.
6. Определяем напряжение 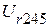 и
и  :
:
 В,
В,
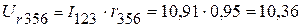 В.
В.
7. Токи  и
и  в схеме цепи, приведенной на рисунке 2.114 а, определяем по закону Ома:
в схеме цепи, приведенной на рисунке 2.114 а, определяем по закону Ома:
 А,
А,  А.
А.
8. Ток 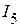 в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 2:
в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 2:
 А.
А.
9. Ток  в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по второму закону Кирхгофа для контура 1421:
в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по второму закону Кирхгофа для контура 1421:
 А.
А.
10. Ток  в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 4:
в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 4:
 А.
А.
11. Ток  в ветви с источником ЭДС в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 1:
в ветви с источником ЭДС в схеме цепи, приведенной на рисунке 2.114 а, определяем из уравнения, составленного по первому закону Кирхгофа для узла 1:
 А.
А.
12. Проверяем решение системы уравнений, составив баланс мощностей.
12.1. Мощность, генерируемая источником напряжения:
 Вт.
Вт.
12.2.Мощность приемников:
 Вт,
Вт,
 Вт,
Вт,
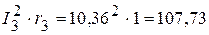 Вт,
Вт,
 Вт,
Вт,
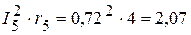 Вт,
Вт,
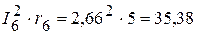 Вт,
Вт,
Суммарная мощность приемников:

 Вт.
Вт.
12.3. Из сравнения генерируемой мощности источниками и потребляемой мощности приемниками, следует, что погрешность вычислений 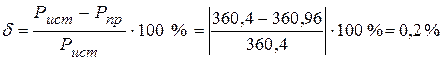 и не превышает 0,5%.
и не превышает 0,5%.






