Уравнения узловых потенциалов можно записать в матричной форме:
,
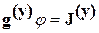где 
- квадратная матрица узловых проводимостей;
- матрица-столбец потенциалов узлов;
- матрица-столбец узловых токов.
Узловой ток i -го узла равен алгебраической сумме тока источника тока и токов, определяемых ЭДС источников напряжений 
.
Уравнение для определения потенциалов узлов имеет вид
,
где 
- матрица, обратная матрице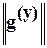 
.
Матрицу узловых проводимостей для соответствующей схемы, можно составить по формуле
,
где 
- матрица соединений;
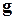- диагональная матрица проводимостей ветвей;
- транспортированная матрица соединений.
Рассмотрим схему, приведенную на рисунке 2.31.
Рисунок 2.31 – Электрическая цепь постоянного тока
Граф электрической цепи приведен на рисунке 2.32.
Рисунок 2.32 – Граф цепи постоянного тока
Так как у приведенной схемы четыре узла, то для нахождения токов в ветвях методом узловых потенциалов, необходимо составить три независимых уравнения. Поэтому, матрица соединения узловых проводимостей ветвей состоит из трех строк и шести столбцов:
.
Диагональная матрица проводимостей 
.
Произведение матриц и 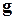равно:
.
Матрица узловых проводимостей получается после перемножения матриц 
и :
.
Матрица-столбец потенциалов узлов 
.
Матрица-столбец узловых токов
.
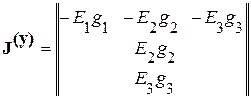Если матрицу дополнить четвертой строкой, соответствующей узлу 4, то получится неопределенная матрица узловых проводимостей цепи, для которой сумма элементов по всем четырем строкам и четырем столбцам равна нулю. Определитель такой матрицы равен нулю. После вычеркивания любой строки и соответствующего этой строке столбца, получается квадратная матрица третьего порядка.
Определитель неопределенной матрицы симметричен относительно главной диагонали. Если вычеркнутая строка не соответствует вычеркнутому столбцу, то и в этом случае получается определенная квадратная матрица, соответствующая независимой системе уравнений. Определитель такой матрицы не имеет симметрии относительно главной диагонали.
Если принять равным нулю потенциал того же узла схемы, которой соответствует вычеркнутой строке матрицы , то напряжения на всех ветвях схемы определяются через потенциалы узлов по формуле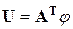 
, где положительное направление напряжения 
совпадает с положительным направлением тока в ветви. Это получается из формул для напряжения каждой ветви. Например, для схемы (рис. 2.31)
.
Из этого выражения следует: 
, 
, 
, 
, 
, 
.
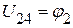Пример 2.13. Решить задачу, приведенную в примере 2.4 с помощью матричных уравнений узловых потенциалов.
Матрица соединений А состоит из пяти строк и десяти столбцов:
.
Диагональная матрица проводимостей
.
Произведение матриц А и 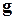равно:
Квадратная матрица узловых проводимостей
.
Матрица-столбец потенциалов узлов
.
Матрица-столбец узловых токов
.
Матрица-столбец ЭДС
.
Определяем матрицу потенциалов узлов схемы
.
Узловые потенциалы токи соответственно равны
В, 
В, 
В,
В, 
В.
Матрица-столбец напряжений ветвей U определяем через матрицу потенциалов узлов схемы :
Матрица токов ветвей 
= 
.
Токи в ветвях соответственно равны
А, 
А, 
А, 
А, 
А,
А, 
А, 
А, 
А, 
А.
Токи, рассчитанные в примерах 2.4 и 2.13, совпадают.
