Метод наименьших квадратов

 

Цель работы: научиться находить аналитическое выражение таблично заданной функции с помощью метода наименьших квадратов.

Задание: найти наилучшее приближение таблично заданной функции.

 

Пусть на основании эксперимента требуется установить функциональную зависимость величины у от величины х:

у=j(х) (1)

Пусть в результате эксперимента получено п значений функции у при соответствующих значениях аргумента. Результаты записаны в таблицу:

 

х			………
			………

Вид функции j (х) устанавливается или из теоретических соображений, или на основании расположения на координатной плоскости точек, соответствующим экспериментальным значениям. Её выбирают обычно из несложных элементарных функций так, чтобы она как можно лучше описывала экспериментальные данные:

 

Вид аппроксимирующей функции	Вид аппроксимирующей функции

При выбранном виде функции у=j (х,а,b,c,…) остается подобрать входящие в нее параметры для наилучшего в некотором смысле приближения функцией рассматриваемого процесса. Эта задача называется сглаживанием (аппроксимацией) экспериментальной зависимости и часто решается методом наименьших квадратов. Сглаживающую кривую называют аппроксимирующей.

Рассмотрим сумму квадратов разностей значений у_i, даваемых экспериментом, и функции j (х,а,b,c,…) в соответствующих точках:

S (a,b,c,…)= (2)

Подбираем параметры a,b,c,… так, чтобы эта сумма имела наименьшее значение:

S (a,b,c,…)= → min (3)

Задача свелась к нахождению значений параметров a,b,c,…, при которых функция S (a,b,c,…) имеет минимум. На основании необходимого признака экстремума функции нескольких переменных

(4)

Для каждой конкретной функции равенства (4) в развернутом виде представляют собой систему уравнений для нахождения неизвестных параметров. Например, для случая, когда в качестве аппроксимирующей функции выбрана линейная у=ах+b, система уравнений имеет вид:

 

,

.

 

Такую систему можно решать любыми способами, том числе и с помощью пакета Mathcad.

 

1. Линейная функция.

 

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде линейной функции .

Решение.

1). Вводим исходные данные задачи в виде массивов и .

2). Сортируем данные, если они даны не в порядке возрастания. Значения запишем соответственно отсортированным значениям , используя функцию (в массив М внести значения и ).

3). Вводим переменные, необходимые для дальнейших вычислений:

4).Находим коэффициенты линейной функции, используя встроенные возможности Mathcad:

Функция позволяет найти угловой коэффициент линии регрессии (наклон линии регрессии), а – смещение по оси ординат линии регрессии (свободный параметр). Их можно найти также, реализовав метод наименьших квадратов, решая для этого систему двух линейных уравнений с двумя неизвестными

В результате получим: значения и , найденные по приближающей линейной функции и полученные решением системы двух уравнений с двумя неизвестными

 

Таким образом, функция имеет вид /

5). Проверим, как точно найден характер исходной функции. Для этого найдем отклонение таблично заданных значений от точек полученной линейной функции

6). Правильность выбора приближающей функции можно определить и по коэффициенту корреляции, используя функцию :

Или записав формулу вычисления коэффициента корреляции:

 

Полученное значение коэффициента показывает, что зависимость у нас обратная (знак «минус») и связь достаточно тесная (число достаточно близко к 1).

 

2. Квадратичная функция.

 

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде многочлена второй степени .

Решение.

 

 

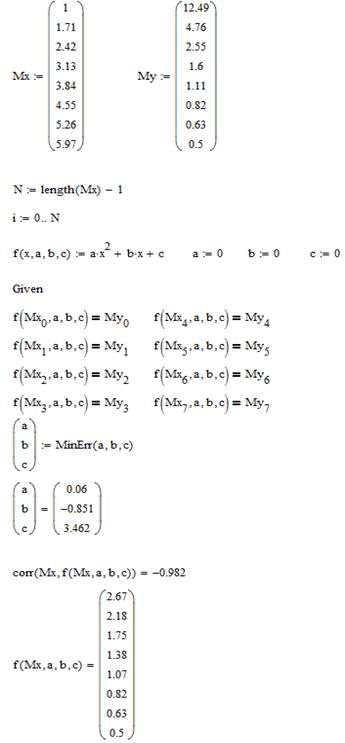3. Степенная функция

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде степенной функции .

 

Решение.

 

4. Показательная функция.

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде показательной функции .

5. Логарифмическая функция.

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде логарифмической функции .

Решение.

6. Гиперболическая функция.

Известны значения функции в некоторых точках, представленных в таблице

 

х		1.71	2.42	3.13	3.84	4.55	5.26	5.97
у	12.49	4.76	2.55	1.60	1.11	0.82	0.63	0.5

 

Найти приближенное выражение функции в виде гиперболы

Решение.

 

 

Задача. Для исходных данных, представленных в таблице, выяснить, какая из функций (линейная, квадратическая, степенная, показательная, логарифмическая, гиперболическая) наиболее точно их описывает

№	Исходные данные для задачи аппроксимации
	х	1,20	1,57	1,94	2,31	2,68	3,05	3,42	3,79
у	2,59	2,06	1,58	1,25	0,91	0,66	0,38	0,21
	х	1,73	2,56	3,39	4,22	5,05	5,89	6,70	7,53
у	0,63	1,11	1,42	1,94	2,30	2,89	3,29	3,87
	х	-4,38	-3,84	-3,23	-2,76	-2,22	-1,67	-1,13	-0,60
у	2,25	2,83	3,44	4,31	5,29	6,55	8,01	10,04
	х	1,00	1,64	2,28	2,91	3,56	4,19	4,84	5,48
у	0,28	0,19	0,15	0,11	0,09	0,08	0,07	0,06
	х	5,84	3,82	6,19	9,22	7,87	6,29	4,43	8,91
у	79,31	57,43	60,66	92,55	90,12	71,30	70,50	91,25
	х	2,91	2,94	6,35	6,58	3,80	6,43	0,57	5,96
у	82,16	61,02	44,56	82,52	99,17	70,24	63,23	66,48
	х	5,46	2,73	6,49	4,26	2,39	6,46	0,86	2,05
у	65,72	58,05	60,05	55,79	50,83	47,69	44,49	59,74
	х	1,28	1,76	2,24	2,72	3,20	3,68	4,16	4,64
у	2,10	2,62	3,21	3,96	4,98	6,06	7,47	9,25
	х	-4,84	-4,30	-3,76	-3,22	-2,68	-2,14	-1,60	-1,06
у	-0,09	-0,11	-0,13	-0,16	-0,19	-0,26	-0,39	-0,81
	х	3,54	4,29	4,78	3,99	1,13	6,29	1,89	3,27
у	22,81	28,42	24,95	26,96	8,78	33,55	15,77	22,80
	х	4,08	4,42	2,52	-0,08	2,14	3,36	7,35	5,00
у	18,31	21,85	16,93	-8,23	10,90	17,18	36,45	24,11
	х	1,16	1,88	2,60	-3,32	4,04	4,76	5,48	6,20
у	0,18	0,26	0,32	0,36	0,40	0,43	0,95	0,85
	х	1,00	1,71	2,42	-3,13	3,84	4,55	5,26	5,97
у	12,49	4,76	2,55	1,60	1,11	0,82	0,63	0,50
	х	-0,64	-0,36	-0,08	0,20	0,48	0,76	1,04	1,32
у	29,51	18,86	12,05	7,70	4,92	3,14	20,1	1,28
	х	-2,45	-1,94	-1,43	-0,92	-0,41	0,10	0,61	1,12
у	0,87	1,19	1,68	2,23	3,04	4,15	5,66	7,72
	х	1,54	1,91	2,28	-2,65	3,02	3,39	3,76	4,13
у	-2,52	-3,08	-3,54	-3,93	-4,27	-4,57	-4,84	-5,09
	х	1,20	2,00	2,80	-3,60	4,40	5,20	6,00	6,80
у	-10,85	-6,15	-4,14	-3,02	-2,30	-1,81	-1,45	-1,17
	х	-1,04	-0,67	-0,30	0,07	0,44	0,81	1,18	1,55
у	10,80	8,08	5,97	4,44	3,31	2,46	1,83	1,36
	х	0,41	0,97	1,53	-2,09	2,65	3,21	3,77	4,33
у	0,45	1,17	1,56	1,82	2,02	2,18	2,31	2,44
	х	3,80	0,25	0,48	5,78	4,91	1,56	0,91	5,73
у	-19,23	-21,41	-9,90	-19,56	-0,30	-12,04	1,14	11,26

Отчет о выполненной работе должен содержать:

1. Тему и цель работы

2. Индивидуальное задание согласно варианту

3. Решение предложенных задач

 

Вопросы к защите лабораторной работы

 

1. Для чего применяется метод наименьших квадратов?

2. Объясните сущность метода наименьших квадратов.

3. Что служит показателем точности аппроксимации?