Далее для краткости будем обозначать абсолютную погрешность числа х как  , относительную погрешность -
, относительную погрешность - 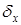 .
.
1. Погрешность суммирования чисел  ,
,  .
.
Абсолютная погрешность:
 .
.
Относительная погрешность:

2. Погрешность вычитания чисел  ,
,  .
.
Абсолютная погрешность:
 .
.
Относительная погрешность:

3. Погрешность умножения чисел  ,
,  .
.
Абсолютная погрешность:
 .
.
Относительная погрешность:

4. Погрешность деления чисел  ,
,  .
.
Абсолютная погрешность:

Относительная погрешность:
 .
.
5. Погрешность функции, зависящей от одной переменной.
Абсолютная погрешность:

Относительная погрешность:

Аналогично получают формулы для оценки абсолютной и относительной погрешности для функций, зависящих от n переменных.
Задание 1: Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:
а) в строгом смысле б) в широком смысле



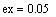





Ответ: абсолютная погрешность для числа х:
относительная погрешность числа х
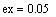

абсолютная погрешность для числа y:
относительная погрешность числа y
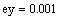

Задание 2. Число х, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата х1 вычислить границы абсолютной и относительной погрешностей. В записи числа х1 указать количество верных цифр по абсолютной и относительной погрешности.







Это значит, что в числе 1.143 три цифры до тысячных (1,1,4,3) верны в строгом смысле по абсолютной погрешности.


т.к. первая значащая цифра в относительной погрешности 3<5, то сравниваем относительную погрешность с числом

Это значит, что в числе 1.143 три цифры (1,1,4) верны в строгом смысле по относительной погрешности.
Задание 3. Вычислить значение величины z с помощью ЭВМ при заданных значениях a и b с систематическим учетом абсолютных погрешностей после каждой операции, если цифры верны в строгом смысле.



Для получения значения величины z необходимо выполнить 6 действий. Будем вычислять абсолютную погрешность после каждого действия с целью определения количества верных цифр в промежуточных результатах.
Т.к. цифры верны в строгом смысле, то абсолютные значения данных чисел a, b равны соответственно:



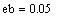
1) 
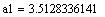

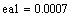

Значит, в числе а1 верны цифры до сотых (т.е.3, 5, 1, а остальные - сомнительные. т.е.

(сохраняем одну сомнительную цифру)
2) 




Значит, в числе b1 верны цифры до десятых (т.е.3, 7, а остальные - сомнительные. т.е.

(сохраняем одну сомнительную цифру)
3) 


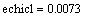

Значит, в числе chicl верны цифры до десятых (т.е.7, 2, а остальные - сомнительные. т.е.

(сохраняем одну сомнительную цифру)
4) 




Значит, в числе а2 верны цифры до тысячных (т.е.2, 5, 1, 2, а остальные - сомнительные. т.е.
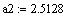
(сохраняем одну сомнительную цифру)
5) 




Значит, в числе chicl верны цифры до единиц (т.е.1, 6, а остальные - сомнительные. т.е.
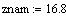
(сохраняем одну сомнительную цифру)
6)





Значит, в числе z верны цифры до сотых (т.е.0, 4, 3, а остальные - сомнительные. т.е.

(сохраняем одну сомнительную цифру)


т.к. первая значащая цифра в относительной погрешности 4<5, то сравниваем относительную погрешность с числом

Это значит, что в числе 0.4339285714 две цифры (4,3) верны в строгом смысле по относительной погрешности.
Ответ: Величина z=0,434. Две цифры 4, 3 верны по абсолютной погрешности, две цифры верны по относительной погрешности.
Задания для самостоятельной работы
Задача 1. Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры (Табл. 1):
а) в строгом смысле, б) в широком смысле.
Таблица 1
| 1. 1 | а)11,445 | б) 2,043 | а) 2,4516, | б) 0,863 | |
| 2. 2 | а) 8,345, | б) 0,288 | а) 5,6432, | б) 0,00858 | |
| 3. 3 | а) 0,374, | б) 4,348 | а) 12,688, | б) 4,636 | |
| 4. 4 | а) 41,72, | б) 0,678 | а) 15,644, | б) 6,125 | |
| 5. 5 | а) 18,357, | б) 2,16 | а) 16,383, | б) 5,734 | |
| 6. 6 | а) 14,862, | б) 8,73 | а) 18,275, | б) 0,00644 | |
| 7. 7 | а) 0,3648, | б) 21,7 | а) 3,75, | б) 6,8343 | |
| 8. 8 | а) 0,5746, | б) 236,58 | а) 26,3, | б) 4,8556 | |
| 9. 9 | а) 5,634, | б) 0,0748 | а) 43,813, | б) 0,645 | |
| а) 20,43, | б) 0,576 | а) 3,643, | б) 72,385 | ||
| а) 12,45, | б) 3,4453 | а) 3,425, | б) 7,38 | ||
| а) 2,3445, | б) 0,745 | а) 0,573, | б) 3,6761 | ||
| а) 0,5746, | б) 42,884 | а) 0,3825, | б) 24,6 | ||
| а) 3,4, | б) 0,078 | а) 0,856, | б) 23,508 | ||
| а) 2,4342, | б) 0,57004 | а) 5,60234, | б) 0,07 | ||
| а) 112,5, | б) 0,04453 | а) 20,4143, | б) 0,51 | ||
| а) 0,576, | б) 2,5008 | а) 12, | б) 53,3 | ||
| а) 25,613, | б) 0,0748 | а) 2.35, | б) 0,74015 | ||
| а) 0,4223, | б) 0,57 | а) 92.451, | б) 103,43 | ||
| а) 112,45, | б) 3,4 | а) 2010.345, | б) 0,44745 |
Задача 2. Число х (Табл. 2), все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата x 1 »x вычислить границы абсолютной и относительной погрешностей. В записи числа x 1 указать количество верных цифр по абсолютной и относительной погрешностям.
Таблица 2
| № | x | № | х |
| 1. 1 | 23,394 | ||
| 2. 2 | 32,147 | 0,003775 | |
| 3. 3 | 35,085 | 718,21 | |
| 4. 4 | 7,544 | 9,73491 | |
| 5. 5 | 198,745 | 11,456 | |
| 6. 6 | 37,4781 | 0,1495 | |
| 7. 7 | 0,183814 | 6,2358 | |
| 8. 8 | 0,009145 | 4,4005 | |
| 9. 9 | 11,3721 | 2,3078 | |
| 0,2538 | 3,2175 | ||
| 10,2118 | 0,0002568 | ||
| 4,394 | 37,8455 | ||
| 0,8437 | 0,09872 | ||
| 129,66 | 3,00971 | ||
| 48,847 | 1,15874 | ||
| 9,2038 | 0,003711 | ||
| 2,3143 | 0,029056 | ||
| 0,012147 | 4,7561 | ||
| 0,86129 | 0,003822 | ||
| 0,1385 | 0,095641 |
Задача 3. Вычислить значение величины z (Табл. 3) при заданных a, b и c c систематическим учетом абсолютных погрешностей после каждой операции и с помощью метода границ. Найти абсолютную и относительную погрешности z, и определить по ним количество верных цифр в z, если цифры a, b и c верны в строгом смысле:
Таблица 3
| № | Задание | Исходные данные | № | Задание | Исходные данные |
| 1. 1 | 
| a = 0,317 b = 3,27 c = 4,7561 | 
| a = 0,038 b = 3,9353 c = 5,75 | |
| 2. 2 | 
| a = 0,0399 b = 4,83 c = 0,0721 | 
| a = 7,345 b = 0,31 c = 0,09871 | |
| 3. 3 | 
| a = 1,0574 b = 1,40 c = 1,1236 | 
| a = 0,2471 b = 0,0948 c = 4,378 | |
| 4. 4 | 
| a = 12,72 b = 0,34 c = 0,0290 | 
| a = 1,284 b = 4,009 c = 3,2175 | |
| 5. 5 | 
| a = 3,49 b = 0,845 c = 0,0037 | 
| a = 18,407 b = 149,12 c = 2,3078 | |
| 6. 6 | 
| a = 0,0976 b = 2,371 c = 1,15887 | 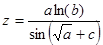
| a = 29,49 b = 87,878 c = 4,403 | |
| 7. 7 | 
| a = 82,3574 b = 34,12 c = 7,00493 | 
| a = 74,079 b = 5,3091 c = 6,234 |
Продолжение таблицы 3
| № | Задание | Исходные данные | № | Задание | Исходные данные |
| 8. 15 | 
| a = 3,71452 b = 3,03 c = 0,756 | 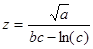
| a = 3,4 b = 6,22 c = 0,149 | |
| 9. 16 | 
| a = 0,11587 b = 4,256 c = 3,00971 | 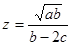
| a = 5,387 b = 13,527 c = 0,7565 | |

| a = 4,05 b = 6,723 c = 0,03254 | 
| a = 1,75 b = 1,215 c = 0,041 | ||

| a = 0,7219 b = 135,347 c = 0,013 | 
| a = 3,672 b = 4,63 c = 0,0278 | ||

| a = 0,113 b = 0,1056 c = 89,4 | 
| a = 13,57 b = 3,7 c = 4,226 | ||

| a = 1,247 b = 0,346 c = 0,051 | 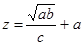
| a = 0,317 b = 13,57 c = 0,751 | ||

| a = 11,7 b = 0,0937 c = 5,081 | 
| a = 0,317 b = 33,827 c = 14,85 | ||

| a = 18,035 b = 3,7251 c = 0.071 | 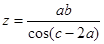
| a = 5,52 b = 3,27 c = 14,123 | ||

| a = 5,7568 b = 21,7 c = 2,65 | 
| a = 9,542 b = 3,128 c = 0,17 |
Отчет о выполненной работе должен содержать:
1. Тему и цель работы
2. Индивидуальное задание согласно варианту
3. Решение предложенных задач
Вопросы к защите лабораторной работы
1.Что такое абсолютная и относительная погрешности?
2.Как классифицируются виды ошибок?
3.Что значит цифра, верная в строгом, широком смыслах?
Лабораторная работа №2,3




