Источниками возникновения погрешности численного решения задачи являются следующие факторы:
- неточность математического описания, в частности, неточность задания начальных данных.
- неточность численного метода решения задачи. Данная причина возникает, например, когда решение математической задачи требует неограниченного или неприемлемо большого числа арифметических операций, что приводит к необходимости ограничения их числа, т.е. использования приближенного решения.
- конечная точность машинной арифметики.
Виды погрешностей
Все погрешности можно разделить на три вида:
- неустранимая погрешность
- погрешность метода
- вычислительная погрешность.
Результирующая погрешность определяется как сумма величин всех перечисленных погрешностей.
Неустранимая погрешность состоит из двух частей:
- погрешность, обусловленная неточностью задания числовых данных, входящих в математическое описание задачи;
- погрешность, являющаяся следствием несоответствия математического описания задачи реальной действительности (погрешность математической модели).
Для вычислителя погрешность задачи следует считать неустранимой, хотя постановщик задачи иногда может ее изменить.
Погрешность метода связана со способом решения поставленной математической задачи. Она появляется в результате замены исходной математической модели другой и/или конечной последовательностью других более простых (например, линейных) моделей. При создании численных методов закладывается возможность отслеживания таких погрешностей и доведения их до сколь угодно малого уровня. Отсюда отношение к погрешности метода как устранимой (или условной).
Вычислительная погрешность (погрешность округлений) обусловлена необходимостью выполнять арифметические операции над числами, усеченными до количества разрядов, зависящего от применения техники.
Рассмотрим пример, иллюстрирующий описанные виды погрешностей. Рассмотрим задачу описания движения маятника, в которой требуется предсказать угол отклонения маятника от вертикали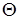 
, начинающего движение в момент времени 
.
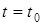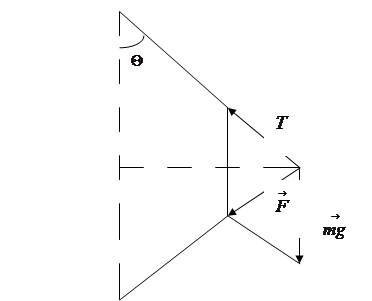
Движение маятника может быть описано дифференциальным уравнением второго порядка:
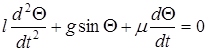(1)
где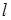 
- длина маятника
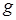- ускорение свободного падения
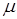- коэффициент трения.
Причины возникновения погрешностей в данной задаче.
- реальная сила трения зависит от скорости движения маятника по нелинейному закону.
- значения величин , , ,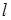 
, 
, 
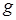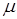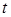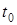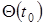известны с некоторыми погрешностями.
- для решения уравнения (1), не имеющего аналитического решения, приходится использовать численный метод, вследствие чего возникает погрешность метода.
- вычислительная погрешность возникает вследствие конечной точности представления чисел в компьютере.
