Существует еще один способ построения трехмерного графика с помощью матрицы значений, которая представляет собой таблицу из трех колонок: в первой будут расположены координаты точек по оси X, во второй -по оси Y, в третьей - по оси Z. В Mathсad существует специальная функция маtrіх(m,n,f) (матрица). Функция формирует матрицу, элементы которой равны значениям функции f(x,y), исходя из того условия, что x=i, y=j (т.е. переменные определяются равными соответствующим матричным индексам данного элемента). Количество строк создаваемой матрицы определяется в первом маркере имени функции (параметр m), количество колонок - во втором (параметр n). Аналогично двумерному случаю, задать поверхность можно, используя оператор ранжированной переменной по готовым матрицам.
Способ построения с помощью специальной матричной
функции CreateMesh
Можно создать график также с помощью специальной матричной функции CreateMesh (Создать сетку).
Функция CreateMesh(F,s,sl,t,tl,sgrіd,tgrіd,fmap) вводится в маркер графической области и имеет пустые маркеры, в которые последовательно вводятся:
– имя матрицы значений или функции F;
– начальное значение первой переменной s;
– начальное значение второй переменной sl;
– конечное значение первой переменной t;
– конечное значение второй переменной tl;
– число линий сетки по первый переменной sgrіd;
– количество линий сетки по второй переменной tgrіd;
– карта отображения frnap.
Кроме поверхностей в пространстве можно задавать и разного рода линии. Для этого существует специальная функция CreateSpace(F,t,tl,tgrіd,frnap) (Создать пространство). Она имеет пять маркеров, в которые последовательно вводятся имя массива данных или системы параметрических уравнений, начальное и конечное значения параметра, количество разбивок промежутка параметра, карта отображения.
Параметрическое закручивание разрешает создавать графики, которые заданы в параметрической форме. Последовательность действий при использовании алгоритма параметрического закручивания следующая.
1. Задать уравнение любой функции f(x).
2. Задать систему параметрического закручивания и соединить ее в один массив:
A(u,v):=u,
B(u,v):=f(u)cos(v),
C(u,v):=f(u)sin(v),

3. Внести в маркер следующую запись: CreateMesh(M, s,sl,t,tl,sgrid,tgrid).
Действия с матрицами
С помощью встроенных функций MathCad матрицы можно объединять, выделять в них подмассивы, определять размеры массивов, максимальные, минимальные значения, нахождение собственных чисел и векторов. Для матриц определенны следующие операции: добавление, произведение, обращение, транспонирование, и т.п..
Создать матрицу можно следующим образом:
записать оператор присваивания, для введения правой части использовать команду Іnsert/Matrіx или на панели инструментов Matrіx. В окне, которое раскроется, задать число строк и столбцов матрицы. Вектор является матрицей с одним столбцом. Ввести значение элементов матрицы в соответствующие места. Дальше можно выполнять все необходимые операции с матрицами
Для работы с элементами матрицы используются индексы элементов. Нумерация строк и столбцов матрицы начинается из нуля. Индекс элемента определяется на панели инструментов Matrіx кнопкой Subscrіpt (рис.1,в), например Mn,k. Два индекса, которые определяют элемент матрицы, отделяются запятой. Номер столбца матрицы отображается как верхний индекс, который заключен в угловые скобки, для чего используется кнопка Column на панели инструментов Matrіx, например, М<1>.
Для проведения операций с матрицами используется меню Symbolіc и команда Matrіx (рис. 12).
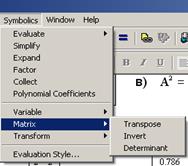
Рисунок 12 – Меню Symbolic для работы с матрицами в символьном
виде.






