При определении влияния собственного веса на деформацию при растяжении и сжатии стержней придется учесть, что относительное удлинение различных участков стержня будет переменным, как и напряжение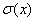 
. Для вычисления полного удлинения стержня постоянного сечения определим сначала удлинение бесконечно малого участка стержня длиной 
, находящегося на расстоянии 
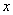от конца стержня (рис.2.20).
Рис.2.20.
Абсолютное удлинение этого участка равно
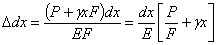
Полное удлинение стержня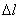 
равно:
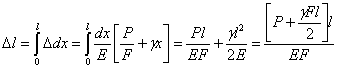
Величина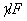 
представляет собой полный вес стержня. Таким образом, для вычисления удлинения от действия груза и собственного веса можно воспользоваться прежней формулой:
подразумевая под S внешнюю силу и половину собственного веса стержня.
Что же касается деформаций стержней равного сопротивления, то, так как нормальные напряжения во всех сечениях одинаковы и равны допускаемым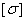 
, относительное удлинение по всей длине стержня одинаково и равно
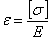
Абсолютное же удлинение при длине стержня l равно:
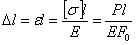
Деформацию ступенчатых стержней следует определять по частям, выполняя подсчеты по отдельным призматическим участкам. При определении деформации каждого участка учитывается не только его собственный вес, но и вес тех участков, которые влияют на его деформацию, добавляясь к внешней силе. Полная деформация получится суммированием деформаций отдельных участков.
Пример 9.
Определить объем кладки мостовой опоры высотой 42 м, нагруженной сжимающей силой F =400 т, для двух вариантов:
1 вариант - опора постоянного сечения;
2 вариант - опора ступенчатая из трех частей одинаковой высоты.
Объемный вес материала кладки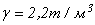 
, расчетное сопротивление материала кладки на сжатие 
.
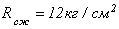Решение.
Объем кирпичной кладки вычисляется по формуле:
,
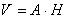где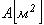 
- площадь поперечного сечения столба; 
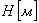- высота столба.
Таким образом, для решения задачи необходимо знать площади поперечных сечений мостовой опоры.
1.Вариант. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.21.
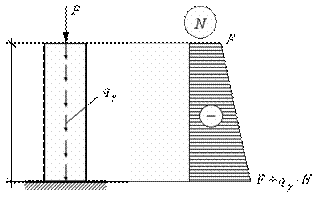
Рис.2.21
Максимальная сжимающая продольная сила возникает у основания опоры и определяется выражением (для удобства будем подставлять значения внутренних усилий по абсолютной величине):
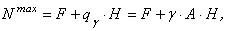
Записываем условие прочности:
Подставляя в это выражение значение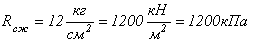 
получим:
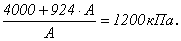
Отсюда требуемая площадь из условия прочности кладки на сжатие равна:
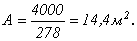
Объем кладки для первого варианта будет равен:
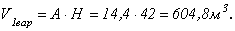
2 вариант. Расчетная схема и эпюра внутренних усилий для данного варианта изображена на рис. 2.22.
Мостовая опора состоит из трех ступеней, высота каждой 
. Площади поперечных сечений ступеней соответственно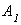 
, 
, 
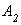, в связи с чем в пределах каждой ступени от действия собственного веса будут возникать различные по величине продольные силы и напряжения.
Таким образом, для решения задачи необходимо рассмотреть условие прочности для каждой ступени отдельно.
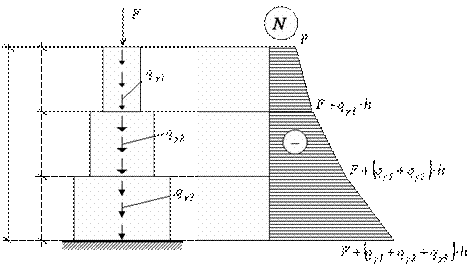
Рис.2.22
1-я ступень. Максимальная сжимающая продольная сила для первой ступени (рис. 2.22):
.
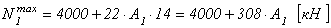По аналогии с вариантом 1, записываем для первой ступени условие прочности и подставляем в него исходные данные:
.
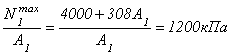Отсюда требуемая площадь первой ступени равна:
2-я ступень. Максимальная сжимающая продольная сила для второй ступени (рис. 2.22):
.
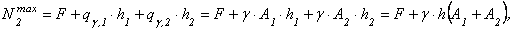
Записываем для второй ступени условие прочности и подставляем в него исходные данные:
.
Отсюда требуемая площадь второй ступени равна:
3-я ступень. Максимальная сжимающая продольная сила для третьей ступени (рис. 2.22):
.
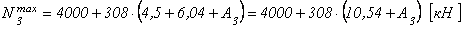Записываем для третьей ступени условие прочности, из которого по аналогии с предыдущими записями определяем требуемую площадь поперечного сечения:
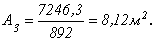
Объем кладки мостовой опоры для второго варианта определяется выражением:
.
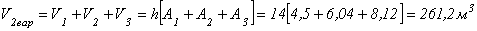Таким образом, мостовая опора, состоящая из ступеней различной площади, выгоднее по расходу материала, чем опора постоянного по всей высоте сечения.
Пример 10.
Определить полное удлинение стержня, с учетом собственного веса, а также перемещение сечения m-n. Площадь поперечного сечения – А, модуль упругости – Е, объемный вес материала -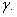 
Расчетная схема стержня изображена на рис. 2.23.
Рис.2.23
Решение.
Для решения задачи используем принцип независимости действия сил, а именно: отдельно построим эпюры продольных сил от действия сосредоточенной силы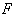 
и от действия собственного веса, то есть от равномерно распределенной продольной нагрузки 
. Расчетная схема и эпюры продольных сил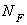 
и 
изображены на рис. 2.23.
Полное удлинение стержня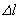 
будет складываться из удлинения, полученного стержнем от действия сосредоточенной силы 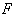и от действия собственного веса:
.
Или в другом виде:
.
Для того, чтобы определить перемещение сечения m-n отбрасываем часть стержня ниже сечения m-n, а ее действие заменяем сосредоточенной силой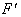 
, равной продольной силе в сечении m-n:
.
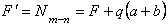В результате получаем новую расчетную схему, которая приведена на рис. 2.24.
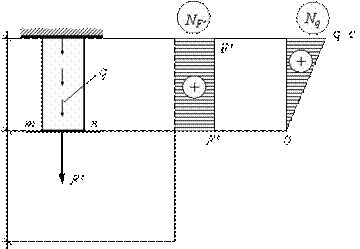
Рис.2.24.
А теперь решаем новую задачу о нахождении полного удлинения 
уже для данного стержня (рис. 2.23):
,
.
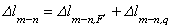