Иногда компоненты девиатора напряжений обозначают:
Шаровой тензор характеризует напряженное состояние всестороннего растяжения – сжатия частицы тела, а девиатор – напряженное состояние её формоизменения.
На каждую частицу тела кроме напряжений действуют объёмные силы:
,
где Rx, Ry, Rz – проекции этих сил на координатные оси. Каждая вектор-сила 
действует на единицу объёма.
На поверхности тела F на каждую единицу её площади могут действовать распределённые силы:
,
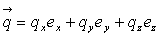где qx, qy, qz – проекции этих сил.
Если последние действуют на малых площадках контакта 
поверхности тела, то их, согласно принципу смягчения граничных условий Сен-Венана, заменяют главными вектором 
и моментом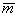 
всех сил, действующих на этих малых площадках:
где 
- радиус – вектор, проведённый из заданной точки (центра приведения сил) на до текущей силы 
.
В результате действия на тело внешних сил , температуры Т каждая точка В совершает перемещение 
в новое положение В ’. Это перемещение характеризуется направленным отрезком 
, т.е. вектором перемещения:
,
где u, v, w – проекции этого перемещения на координатные оси.
Перемещения характеризуют деформацию тела в целом. Например, прогибы точек оси балки V и поворот поперечных сечений, проходящих через эти же точки, характеризуют деформацию балки в целом при её изгибе.
Деформация тела складывается из деформации её материальных (физических) частиц, каждая из которых испытывает удлинения 
в направлении её рёбер и искажения прямых углов:
между её гранями в каждой из координатных плоскостей (рис. 3.2).
Величины
называют относительными удлинениями или деформациями частиц тела. Половины сдвигов обозначают:
.
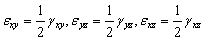Совокупность шести компонентов деформации полностью характеризует деформированное состояние частицы тела. Эту совокупность запишем в виде квадратной матрицы:
(7)
и назовем тензором деформаций Коши.
а) б)
Рис. 3.2
Величину
(8)
называют средней деформацией.
Если для рассматриваемого тензора деформация 
, то он называется тензором-девиатором или просто девиатором деформации.
В общем случае 
тензор (7) можно разложить на сумму двух тензоров:
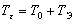
Первый из них:
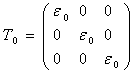(9)
носит название шарового тензора деформации и описывает объёмную деформацию всестороннего растяжения – сжатия.
Второй тензор:
(10)
представляет собой тензор-девиатор и характеризует деформацию изменения формы частиц тела.
Основные виды напряжённо-деформированного состояния (НДС)
До сих пор мы рассматривли в основном простейшие виды НДС – растяжение – сжатие, плоский чистый сдвиг и их комбинацию (рис. 3.3).
а) б) в)
Рис. 3.3
Они встречаются при растяжении и сжатии стержня и его кручении, а также при изгибе (рис. 3.4). При растяжении и сжатии (рис. 3.4, а) осевая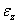 
и поперечные деформации 
, 
определяются законами Гука и Пуассона:
(11)
А) Растяжение б) Кручение
В) Изгиб
Рис. 3.4
При плоском чистом сдвиге (рис. 3.4, б) деформация сдвига
(12)
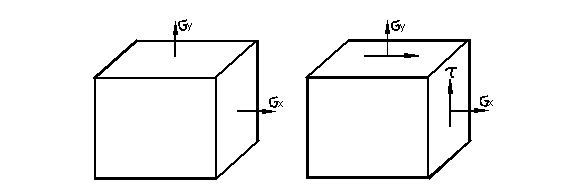
Часто на практике встречаются двухосное растяжение и его комбинация с чистым сдвигом (рис. 3.5).
а) б)
Рис. 3.5
В последнем случае состояние называют плоским напряжённым состоянием. Оно возникает в тонкостенных элементах конструкций, таких как плиты (пластины) и оболочки (рис. 3.6).
При двухосном растяжении деформации в направлениях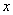 
и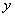 
могут быть найдены на основании законов (11) для одноосного растяжения. Представим , на основании принципа независимости действия сил (напряжений 
, 
) в виде суммы деформаций в каждом из направлени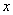й и 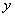от этих сил:
(13)
а) б)
Рис. 3.6
Для плоского напряжённого состояния (рис. 3.6, б) с учётом (12) получаем:
(14)
При трёхосном растяжении (рис. 3.7, а) на основании законов (11) аналогичным образом получаем:
(15)
