Расчет конструкций по допускаемым нагрузкам.

Расчет статически определимых систем по способу допускаемых нагрузок.

В предыдущем изложении методов расчета мы исходили из основного условия прочности . Это неравенство требует выбора размеров конструкции с таким расчетом, чтобы наибольшее напряжение в самом опасном месте не превосходило допускаемого.

Но можно стать на другую точку зрения. Можно задать условие, чтобы действительная нагрузка на всю конструкцию не превосходила некоторой допускаемой величины. Условие это можно выразить таким неравенством:

За допускаемую нагрузку надо выбрать некоторую 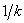часть той нагрузки, при которой конструкция перестанет функционировать правильно, перестанет выполнять свое назначение. Такая нагрузка обычно называется предельной, иногда— разрушающей в широком смысле слова (под разрушением конструкции подразумевают прекращение ее нормальной работы).

В качестве примера возьмем систему из двух стальных стержней АВ и АС (рис.2.56), нагруженных силой P.

 

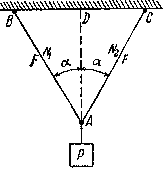
Рис.2.56

 

Рассчитывая эту систему обычным путем, найдем усилия N₁ = N₂ no формуле:

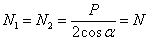
(из равновесия узла А). Отсюда площадь каждого из стержней равна:

По способу допускаемых нагрузок имеем:

Введя в качестве коэффициента запаса для конструкции в целом ту же величину k, которая была принята в качестве коэффициента запаса для напряжений, мы получим, что величина

Предельной, опасной величиной P_пр будет та, при которой напряжения в стержнях дойдут до предела текучести:

Таким образом, допускаемая величина Р равна:

Условие прочности принимает вид

а учитывая, что

,

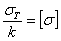получаем:

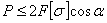
Отсюда:

Таким образом, расчет по допускаемым нагрузкам привел в данном случае к тем же результатам, что и расчет по допускаемым напряжениям. Это всегда имеет место для статически определимых конструкций при равномерном распределении напряжений, когда материал по всему сечению используется полностью.

 

 

.

 

Вопросы для самопроверки

- Что называется стержнем?

- Какой вид нагружения стержня называются осевым растяжением (сжатием)?

- Какие внутренние силовые факторы возникают в сечении бруса при растяжении и сжатии?

- Как распределяются по сечению силы упругости при растяжении и сжатии? (Использовать гипотезу плоских сечений.)

- Как вычисляется значение продольной силы в произвольном поперечном сечении стержня?

- Какого характера напряжения возникают в поперечном сече­нии при растяжении и сжатии: нормальные или касательные?

- Как распределены нормальные напряжения в поперечных сечениях центрально-растянутого или центрально-сжатого стержня и по какой формуле они определяются?

- Получите формулу нормальных напряжений при растяжении-сжатии? Какие предпосылки используются при вы­воде этой формулы?

- Как записывается условие прочности бруса при растяжении (сжатии)? Какие виды задач решаются с помощью условия прочности?

- В каких единицах измеряется напряжение?

- Как изменится величина напряжения, если площадь поперечного сечения возрастет в 4 раза?

- Как назначаются знаки продольной силы и нормального на­пряжения?

- Как связаны гипотеза плоских сечений (гипотеза Бернулли) и закон распределения нормальных напряжений в поперечном сечении растянутого (сжатого) стержня?

- Раскройте понятие эпюр продольных сил, нормальных напряжений и перемещений. Для чего они строятся?

- Что показывает эпюра продольной силы?

- Что представляют собой эпюры внутренних силовых факторов? С какой целью их строят?

- Опишите технику построения эпюры продольных сил в брусе, загруженном несколькими сосредоточенными силами по оси бруса?

- Как вычислить значение продольной силы в произвольном поперечном сечении бруса?

- Как вычислить напряжения в поперечном сечение бруса при растяжении и сжатии? Как они распределены по поперечному сечению?

- Как определяют абсолютное удлинение ступенчатого бруса, нагруженного несколькими силами?

- Как определяется удлинение призматического бруса от собственного веса?

- Какое влияние оказывает собственный вес стержня при проектирования сооружения?

- Что понимается под брусом равного сопротивления?

- Запишите формулы для определения удлинения бруса. Что характеризует произведение АЕ и как оно называется?

- Какие деформации бруса называются абсолютными и какие относительными?

- Что называется удлинением стержня (абсолютной продольной деформацией)? Что такое относительная продольная деформация? Каковы размерности абсолютной и относительной продольных деформаций?

- Опишите технику определения продольных и поперечных деформаций бруса при растяжении-сжатии?

- Стальной стержень длиной 1,5 м вытянулся под нагрузкой на 3 мм. Чему равно относительное удлинение? Чему равно относительное сужение? ( = 0,25)

- Что характеризует модуль упругости материала? Какова единица измерения модуля упругости?

- Что называется модулем упругости Е? Как влияет величина Е на деформации стержня?

- Что называется жесткостью поперечного сечения стержня при растяжении (сжатии)?

- Относительные деформации и перемещения.

- Что понимается под жесткостью при растяжении или сжатия стержня?

- Принципы расчета на жесткость.

- Типы задач при расчетах на жесткость.

- Примеры влияния жёсткости на работоспособность конструкции.

- Сформулируйте закон Гука. Напишите формулы для абсолютной и относительной продольных деформаций стержня.

- Что происходит с поперечными размерами стержня при его растяжении (сжатии)?

- Что характеризует коэффициент поперечной деформации?

- Что такое коэффициент Пуассона? В каких пределах он изменяется?

- Как определяется коэффициент Пуассона?

- Какая разница между статически определимой и статически неопределимой стержневой системой?

- Какие системы называют статически неопределимыми? Как установить степень статической неопределимости системы?

- Во сколько раз (примерно) поперечная деформация меньше продольной при осевом растяжении (сжатии) стальных стержней?

- При проведении испытаний были получены различные значения коэффициента Пуассона для стали: 0,15; 0,28; 0,4. Укажите, какие значения ошибочны?

- Вычислите продольную силу, возникающую в поперечном сечении растянутого стержня, если нормальные напряжения в этом сечении равны 140 МПа, а его площадь составляет 100 мм²?

 

- Укажите деформированное состояние стержня, нагруженного осевой силой, если его поперечные размеры увеличились?

1) стержень растянут;

2) стержень сжат.

 

- На рисунке изображён стержень, находящийся под действием растягивающей силы.

Большие напряжения возникнут в точке

1) C;

2) D?

 

- Выберите формулу закона Гука при растяжении (сжатии)?

1) ;

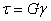2) ;

3) ;

4) .

 

- Какие внутренние усилия возникают при растяжении (сжатии)?

1) поперечная сила,

2) продольная сила.

 

- Что связывает закон Гука при растяжении (сжатии)?

1) продольную и поперечную силу,

2) напряжение и деформацию.

 

- Что является характеристикой жесткости при растяжении?

1) модуль упругости первого рода,

2) модуль упругости второго рода.

 

- Условие жесткости:

1) рабочее напряжение должно быть меньше временного сопротивления;

2) относительная деформация: линейная , угловая ;

3) относительная линейная и угловая деформации одинаковы численно.

 

- При растяжении (сжатии):

1) ;

2) ;

3) , .

 

- Три вида задач из условия жесткости:

1) определение линейных размеров;

2) проверка на условие жесткости; определение размеров сечения; определение максимально допустимых размеров;

3) определение изменения объема конструкции.

 

- Выбор сечения из условия жесткости

1) сечение должно удовлетворять как условию прочности, так и жесткости;

2) сечение должно удовлетворять только условию прочности;

3) сечение должно удовлетворять только условию жесткости.

 

- При расчетах на жесткость получают:

1) гибкость стержня;

2) твердость материала;

3) линейные и угловые деформации.

 

- Какие напряжения возникают в поперечном сечении при растяжении (сжатии)?

1) сжимающие,

2) касательные,

3) продольные,

4) нормальные,

5) изгибающие.

 

- Как определяются напряжения при осевом растяжении (сжатии)?

1) ;

2) ;

3) ;

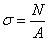4)

 

- Что характеризует жесткость при растяжении (сжатии)?

1) модуль упругости второго рода,

2) модуль упругости первого рода,

3) коэффициент Пуассона.

 

- Какие характеристики связывает закон Гука при растяжении (сжатии)?

1) силу и напряжение,

2) касательное и нормальное напряжение,

3) напряжение и деформацию.

 

- Что связывает поперечную и продольную деформацию при растяжении (сжатии)?

1) модуль упругости,

2) модуль сдвига,

3) коэффициент Пуассона.

 

- Что характеризует произведение ЕА при растяжении (сжатии)?

1) твердость материала,

2) жесткость материала,

3) жесткость стержня.

 

- В каких сочетаниях растянутого бруса возникают наибольшие нормальные, и в каких наибольшие касательные напряжения?

1) Наибольшие нормальные напряжения возникают в поперечных сечениях бруса. Наибольшие касательные возникают в сечениях под углом =45°.

2) Наибольшие нормальные напряжения возникают в сечениях под углом =45°. Наибольшие касательные напряжения в поперечных сечениях бруса.

3) Наибольшие нормальные напряжения возникают в сечениях под углом =0°. Наибольшие касательные напряжения возникают под углом =45°.

4) Наибольшие нормальные напряжения возникают в сечениях бруса под углом =90°. Наименьшие касательные напряжения возникают под углом =0°.

 

- Что называется жесткостью поперечного сечения при растяжении (сжатии)?

1) Жесткостью называется такое состояние материала, при котором деформации ниже допустимых величин.

2) Отношение называется жесткостью поперечного сечения.

3) Произведение называется жесткостью поперечного сечения.

4) Произведение называется жесткостью поперечного сечения.

 

- Назовите единицы измерения коэффициента Пуассона?

1) Н/м².

2) Па.

3) безразмерная величина.

4) м/Н.

 

- Наибольшее по модулю напряжение равно, полагая

1)

2)

3)

4)

 

 

- Если F = 30 кН, А ₁ = 5 см², l = 0,5 м, Е = 200 ГПа, то удлинение стержня 1 (в мм) составит

1) 0,1

2) 0,2

3) 0,3

4) 0,5

 

- Если F = 250 кН, А = 25 см², l = 0,5 м, Е = 200 ГПа, а = 0,4 м, то изменение длины среднего участка (в мм) составит

1) 0,2

2) 0,3

3) 0,4

4) 0,5

 

- Стержни кронштейна, изготовленные из одного материала с коэффициентом линейного расширения нагреваются на градусов. При этом вертикальное перемещение узла В составит, полагая .

1)

2)

3)

4)

 

- Ступенчатый брус при нагружении заданными силами укоротится на величину, кратную

1)

2)

3)

4)

- Наибольшее напряжение в конструкции равно, полагая

1)

2)

3)

4)

 

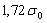
- Считая перемещение влево положительным и полагая , определите перемещение сечения В

1)

2)

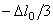
3)

4)

 

- Если предел текучести материала стержней равен , то при нагружении заданной силой F запас прочности конструкции равен, полагая

1)

2)

3)

4)

 

- При нагружении бруса заданными силами наибольшее по модулю напряжение (в МПа) равно

1) 250

2) 220

3) 200

4) 160

 

- Наибольшее по модулю напряжение в брусе равно, полагая

1)

2)

3)

4)

 

- Тензометр Т, прикрепленный вдоль оси стержня 1, показывает деформацию = 4·10^-4. Чему равна величина силы F (в кН), если площадь поперечного сечения стержня А = 10 см²,и модуль Юнга Е = 200 ГПа?

1) 60

2) 70

3) 80

4) 90

 

- Если F = 320 кН, А = 40 см², = 240 МПа, то запас прочности бруса по пределу текучести равен

1) 1,5

2) 1,6

3) 2,0

4) 3,0

 

- Если А ₁ = 10 см², А ₂ = 16 см², [ ] = 160 МПа, то грузоподъемность кронштейна G (в кН) равна

1) 160

2) 172

3) 181

4) 190

 

- Если F = 200 кН, = 200 МПа, А ₁ = 16 см², = 340 МПа, А ₂ = 10 см², то фактический запас прочности конструкции равен

1) 1,5

2) 1,6

3) 1,7

4) 1,8

 

- При нагружении заданной стержневой системы силой F отношение удлинений стержней 1 и 2 численно равно

1) 2,0

2)

3) 0,5

4)