Напряжённое и деформированное состояние частицы тела
Теория НДС ставит своей задачей определение внутренних напряжений, деформаций и перемещений в различных точках деформируемого твёрдого тела произвольной формы и размеров.
Напряженным состоянием тела в точке называют совокупность нормальных и касательных напряжений, действующих по всем площадкам (сечениям), содержащим данную точку.
Отнесём тело к координатным осям x, y, z и выделим мысленно из него материальную частицу в виде параллелепипеда или кубика размерами dx, dy, dz (рис. 3.1)
а) б)
Рис. 3.1
Действия отброшенной части тела заменим векторами – напряжениями 
и разложим их на составляющие по координатным осям.
(1)
где ex, ey, ez - единичные векторы, направленные вдоль координатных осей x, y, z; 
, 
, 
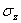- нормальные напряжения, 
, 
, 
, 
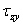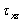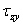, - касательные напряжения. У касательных напряжений первый индекс указывает на направление его действия, второй индекс – на нормаль к площадке, на которой оно действует. У нормальных напряжений индекс соответствует одновременно как направлению, так и нормали к площадке их действия. На невидимых на рис. 3.1 гранях частицы действуют такие же, но противоположно направленные напряжения.
Совокупность указанных напряжений полностью характеризует напряжённое состояние частицы тела. Эту совокупность записывают в виде квадратной матрицы
(2)
и называют тензором напряжений Коши. Система напряжений, приложенных к частице тела, должна удовлетворять условиям равновесия. Первые три условия в проекциях на оси x, y, z дают тождества, т.к. на противоположных гранях мы считаем напряжения равными по величине. Остаётся проверить, обращаются ли в нуль суммы моментов всех сил относительно координатных осей. Составим условие равновесия моментов относительно оси х:
откуда следует 
Аналогично можно составить два уравнения равновесия моментов относительно осей y и z. В результате получим соотношения:
(3)
которые называют законом парности касательных напряжений: на двух взаимно перепендикулярных площадках составляющие касательных напряжений, ортогональные их общему ребру, равны по величине и направлены оба либо к ребру, либо от него. На основании этого закона тензор-матрица напряжений 
является симметричной относительно главной диагонали, состоящей из нормальных напряжений.
Напряжение
(4)
называют средним напряжением. Тензор напряжений, для которого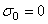 
, называется тензором–девиатором напряжений. В общем случае тензор напряжений можно разложить на сумму двух тензоров:
Первый из них
(5)
носит название шарового тензора напряжений, а второй:
(6)
