Статически определимый стержень – это стержень, который можно рассчитать, используя только уравнения равновесия (уравнения статики).
В любой науке, которая называется «точной» и в которой используются аналитические методы описания состояний и явлений, не обойтись без моделей. В нашем случае при решении различных задач мы каждый раз будем выбирать для рассматриваемого объекта расчетную схему.
Расчетная схема – это упрощенная схема конструкции или ее элементов, освобожденная от несущественных в данной задаче особенностей. При этом расчетная схема должна отражать все наиболее существенное для характера работы данной конструкции и не содержать второстепенных факторов, мало влияющих на результаты ее расчета. Построение и обоснование расчетной схемы – ответственный этап проектирования и расчета конструкции.
Перейдем к рассмотрению конкретных примеров.
Пример 5.
Чугунная труба-стойка высотой 
с наружным диаметром 
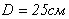и внутренним диаметром 
нагружена сжимающей силой 
, модуль упругости чугуна 
. Найти напряжение 
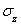в поперечном сечении колонны, абсолютное 
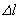и относительное укорочения 
.
Решение.
Как уже говорилось выше, решение задачи начинается с выбора расчетной схемы. В данном случае стойка изображается как вертикальный стержень длиной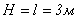 
, жестко закрепленный в нижней части (условное изображение фундамента или земли). К верхней части стержня приложена сосредоточенная сжимающая сила (направление к стержню). При этом линия действия силы должна совпадать с осью стержня. Кроме того, рядом необходимо изобразить поперечное сечение стойки с указанием основных размеров. В данном примере – это кольцо. Расчетная схема для решения задачи изображена на рис. 2.13, а.
Далее строим эпюру продольной силы и определяем максимальное внутреннее усилие, возникающее в колонне. Поскольку внешняя нагрузка постоянна по высоте, то возникает только одна сжимающая продольная сила 
.
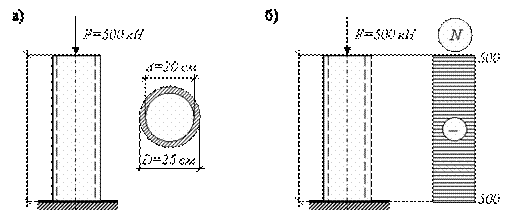
Рис. 2.13.
Максимальное нормальное напряжение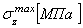 
определяется по формуле:
где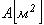 
– площадь трубы:
.
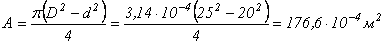тогда:
Абсолютное и относительное укорочения стойки определяем по формулам:
Знак "минус" обозначает уменьшение размера (укорочение).
Пример 6.
Стальной стержень круглого сечения растягивается усилием 
. Относительное удлинение не должно превышать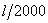 
, а напряжение – 
. Найти наименьший диаметр, удовлетворяющий этим условиям, если модуль упругости стали 
.
Решение.
Как и ранее, решение задачи начинается с изображения расчетной схемы и построения эпюра продольных сил (рис. 2.14).
Рис.2.14
По условию задачи напряжение не должно превышать , в связи с чем данная величина может быть принята за расчетное сопротивление материала стойки на растяжение, то есть 
. По аналогии заданное относительное удлинение можно принять за предельно допустимое для данной стойки, то есть 
. В результате необходимо подобрать диаметр стойки, удовлетворяющий условию прочности и условию жесткости.
Продольное растягивающее усилие равно по величине внешней нагрузке, действующей на стержень 
Требуемая площадь поперечного сечения колонны из условия прочности будет определяться выражением:
Зная требуемую площадь, выразим необходимый из условия прочности диаметр:
Условие жесткости при центральном растяжении-сжатии:
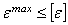
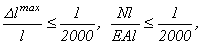
Выражаем из предельного неравенства требуемую из условия жесткости площадь поперечного сечения:
Диаметр стойки из условия жесткости определим по формуле:
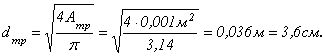
Окончательно принимаем из двух диаметров больший, 
Пример 7.
Определить грузоподъемность и удлинение балки, если 
.
Расчетная схема бруса и эпюра продольных сил изображены на рис. 2.15.
Рис.2.15
Решение.
Грузоподъемность бруса – это максимальная нагрузка, которую он может выдержать, не разрушаясь. Таким образом, необходимо определить требуемую нагрузку из условия прочности:
Согласно эпюре 
, тогда условие прочности примет вид:
Отсюда грузоподъемность бруса будет равна:
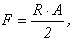
Для определения удлинения стержня 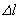разбиваем его на участки. Каждый участок, должен иметь постоянную жесткость 
и величину продольной силы. Таким образом, для данного бруса получаем три участка (на рис. 2.15 они обозначены римскими цифрами), тогда абсолютная деформация в общем виде будет определяться выражением:
,
в котором каждое слагаемое определяется отдельно:
где 
- значения продольных сил соответственно на первом, втором и третьем участках; 
- длины соответственно первого, второго и третьего участков; 
- значения модулей упругости материалов бруса для каждого участка; 
- площади поперечных сечений стержня на первом, втором и третьем участках.
Поскольку жесткости всех трех участков одинаковые (балка изготовлена из одного материала и имеет постоянное по всей длине поперечное сечение), можно обозначить 
и вынести этот множитель за скобки. В результате получим выражение в виде:
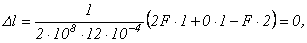
где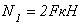 
, 
, 
, 
, 
.
Пример 8.
Проверить прочность чугунного бруса (рис.2.16, а). Принять 
=150 МПа; 
=650 МПа, допускаемый коэффициент запаса прочности 
= 4.
Решение.
Строим эпюры продольных сил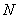 
и нормальных напряжений 
(рис.2.16, б и в).
Рис.2.16
Напряжения на участках бруса
Так как материал бруса имеет различную прочность при растяжении и сжатии, проверку прочности следует выполнять для сжатого и растянутого участков, несмотря на то, что на участке 
напряжение значительно больше по абсолютному значению.
Коэффициенты запаса прочности
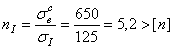
- прочность обеспечена;
- прочность обеспечена.
Из решения задачи можно сделать следующие выводы:
1) прочность стержня не обеспечена, так как на одном его участке коэффициент запаса прочности меньше требуемого;
2) на участках и 
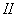коэффициент запаса прочности завышен, следовательно, эти участки бруса можно сделать меньшего диаметра. При проектировании элементов конструкций следует стремиться к тому, чтобы во всех сечениях коэффициент запаса прочности был равен или близок к требуемому.
Проверку прочности бруса можно было выполнить, используя условие прочности в виде 
, определив предварительно допускаемые напряжения по формулам
; 
.
