Изучение затухающих электромагнитных

КОЛЕБАНИЙ В КОНТУРЕ

Цель работы: изучить затухающиеэлектромагнитные колебания в контуре.

Приборы и принадлежности: генератор затухающих колебаний, осциллограф.

 

Сведения из теории

Цепь, состоящую из последовательно соединенных резистора (R), конденсатора (С ) и индуктивности (L), называют колебательным контуром (рис. 10.1).

Периодический процесс преобра­зо­ва­ния энергии электрического поля заряженного конденсатора в энергию магнитного поля катушки индуктивности и обратно называют электромагнитными колебаниями. Свободные электромагнитные колебания в любом ре­аль­ном контуре всегда затухающие. Пер­во­на­чальный запас энергии контура в процессе колебаний расходуется на нагревание проводов, по которым течет ток.

Запишем второй закон Кирхгофа для данного контура

 

.

 

Разделив это уравнение на L и заменив 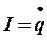, а , получим

 

(10.1)

 

Обозначим , . С учетом этих обозначений уравнение (10.1) примет вид

. (10.2)

 

Решением этого дифференциального уравнения является функция (при условии, что b < w ₀)

q = q _o e^{- b t} cos ( w t + a ). (10.3)

 

Из решения следует, что заряд на пластинах конденсатора меняется по гармоническому закону. Амплитуда колебаний со временем убывает по экспоненте.

Циклическая частота колебаний

 

. (10.4)

 

Нетрудно показать, что напряжение на пластинах конденсатора и ток в контуре меняются по гармоническому закону, аналогичному (10.3).

Период колебаний

. (10.5)

 

Если b (его называют коэффициентом затухания) много меньше w₀, то период колебаний определяется по формуле Томсона

 

. (10.6)

Описание установки

Для получения затухающих электромагнитных колебаний исполь-зуется устройство, схема которого представлена на рис. 10.2. Оно назы­ва­ет­ся генератором затухающих электромагнитных колебаний (ГЗК).

От источника переменного напряжения через сопротивление R ₁ и диод Д заряжается конденсатор С ₁, который является источником постоянного напряжения. От источника постоянного напряжения через сопротивление R ₂ заряжается конденсатор С ₂. После того, как напряжение на конденсаторе С ₂ достигнет величины зажигания неоновой лампы, она вспыхивает и происходит разряд конденсатора С ₂ через неоновую лампу. После снижения напряжения на конденсаторе С ₂ до напряжения гашения неоновой лампы разряд этого конденсатора прекращается и начинается его следующий заряд через сопротивление R ₂. При многократных разрядках и зарядках конденсатора С ₂ в цепи С ₂, R ₃, L возникают затухающие колебания.

Установка ГЗК позволяет менять параметры контура, а следова­тельно, получать различные затухающие колебания.

 

Порядок выполнения работы

1.Подготовить осциллограф к измерениям. Это описано в лабораторной работе № 1.

2. Получить осциллограмму затухающих колебаний.

2.1. Ручку осциллографа “Вольт/дел.” поставить в положение 1.

2.2. Ручку С ГЗК поставить в положение 1¸5 по указанию препо­давателя.

2.3. Ручку R (ГЗК) - в положение 5.

2.4. Ручку L (ГЗК) - в положение 5.

2.5. Ручку осциллографа “Время/дел.” поставить в положение 0,1 ms, ручку “Плавно” - в крайнее правое положение.

2.6. Ручками “Синхр.” в положении “Внутрь” и ручками “Стаб.” и “Уровень” добиться четкой и устойчивой осциллограммы.

2.7. Определить период (Т ) колебаний по осциллограмме. (Определение периода показано в лабораторной работе № 1).

2.8. Определить этот же период по теоретической формуле Томсона (Т _т).

2.9. Определить относительную погрешность измерения периода по формуле

.

 

3.Определить зависимость периода колебаний Т от индуктивности L.

3.1. Меняя индуктивность L в заданных пределах ГЗК, определить период Т для пяти положений ручки L. Результаты занести в табл. 10. 1.

 

Таблица 10.1

 

R =...; C =...;
L
T

 

3.2. Построить график зависимости Т = f (L).

4. Определить зависимость периода колебаний Т от емкости С.

4.1. Установить ручку L (ГЗК) в положение 1¸5 по указанию преподавателя.

4.2. Меняя емкость в заданных пределах ГЗК, определить пять значений периода. Результаты занести в табл. 10. 2.

Таблица 10.2

 

R=...; L=...;
C
T

 

4.3. Построить график зависимости Т = f (С).

5. Меняя сопротивление ГЗК ручкой R, посмотреть, как меняется затухание колебаний. Сделать вывод.

 

КОНТРОЛЬНЫЕ ВОПРОСЫ

 

1. Вывести дифференциальное уравнение, описывающее собственные затухающие колебания в контуре.

2. Декремент и логарифмический декремент затуханий, коэффициент затуханий.

3. Период колебаний, частота колебаний.

4. Время релаксации и добротность контура.

 

ЛАБОРАТОРНАЯ РАБОТА № 11