Изучение явлений электромагнитной индукции и взаимоиндукции

Цель работы: экспериментальная проверка закона Фарадея и некоторых следствий, вытекающих из него.

Приборы и принадлежности: лабораторная установка, состоящая из соленоида и четырех катушек, милливольтметра, амперметра, осцил-лографа и блока питания.

Сведения из теории

Явление электромагнитной индукции. В 1831 году английский физик М. Фарадей открыл явление, заключающееся в том, что при всяком изменении магнитного потока, пронизывающего площадку, ограниченную замкнутым проводящим контуром, в нем возникает электрический ток. Это явление называется явлением электромагнитной индукции, а возникающий ток - индукционным током. Этот факт свидетельствует о том, что при изменении магнитного потока в контуре возникает электродвижущая сила e _i . Опыт показал,что e _i (ЭДС индукции) зависит от скорости изменения магнитного потока, пронизывающего данный контур, т. е.

. (8.1)

 

Магнитный поток, пронизывающий контур, определяется выражением

 

Ф = В S сos a, (8.2)

 

где - вектор индукции магнитного поля; S - площадь контура; a - угол между вектором и положительной нормалью к площадке.

Индукция и напряженность магнитного поля связаны соотношением

 

,

 

где m - магнитная проницаемость; m₀ - магнитная постоянная.

Если контур содержит N витков, то e _i определяется выражением

 

. (8.3)

 

Величина Y называется потокосцеплением, или полным магнитным потоком,

Y = N Ф. (8.4)

Соленоид. Соленоидом называется контур, состоящий из N витков одинакового радиуса, расположенных вплотную друг к другу. В теории рассматривается бесконечный соленоид, состоящий из бесконечного числа витков.

Известно, что индукция магнитного поля в любой точке внутри бесконечного соленоида

В = m m₀ n I, (8.5)

 

где I - ток, текущий по соленоиду; n - число витков на единицу длины соленоида. Если соленоид конечной длины, то индукция в любой точке любого сечения

, (8.6)

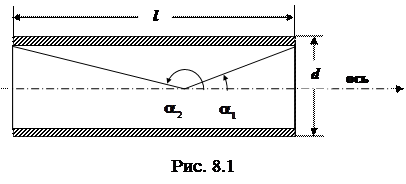
где a₁ и a₂ - углы между осью соленоида и радиусами - векторами, проведенными из любой точки на оси соленоида к его концам (рис.8.1).

Взаимоиндукция. Частным случаем явления электромагнитной индукции является явление взаимоиндукции, которое имеет место тогда, когда два контура расположены достаточно близко друг к другу (рис.8.2). При протекании переменного тока I ₁ по первому контуру во втором контуре возникает ЭДС индукции, которая определяется по формуле

 

, (8.7)

 

здесь Ф₂₁ - магнитный поток, пронизывающий второй контур (создается током I ₁); L ₂₁ - коэффициент взаимоиндукции второго контура с первым. Если создать переменный ток I₂ во втором контуре, то в первом контуре наведется ЭДС индукции:

 

, (8.8)

 

где Ф₁₂ - магнитный поток, прони­зы­ва­ю­щий первый контур (Ф₁₂ создается то­ком I ₂); L ₁₂ - коэффициент вза­имо­ин­дукции первого контура со вторым.

Теоретически доказано, что L ₂₁ = L ₁₂. Если это так, то при поочередном протекании одинаковых переменных токов в двух связанных контурах, ЭДС индукции, возникающие в них, должны быть равны, т. е. e _i2 = e _i1.