КРУГОВОГО ТОКА
Цель работы: исследовать магнитное поле кругового тока с помощью флюксметра.
Приборы и принадлежности: круговой проводник на подставке, амперметр, флюксметр, реостат, источник низковольтного переменного напряжения.
Сведения из теории
В 1820 году датским физиком Эрстедом было обнаружено магнитное поле тока. Магнитное поле является одной из форм материи. Оно характеризуется вектором магнитной индукции 
и вектором напряженности 
магнитного поля. Эти величины для однородной и изотропной среды связаны соотношением
.
Магнитная индукция является силовой характеристикой магнитного поля и численно равна силе, действующей со стороны поля на единицу длины проводника, по которому течет ток единичной силы и который расположен перпендикулярно направлению магнитного поля. Магнитная индукция является характеристикой результирующего магнитного поля в веществе. Напряженность магнитного поля 
не зависит от свойств среды и является характеристикой поля, создаваемого внешними по отношению к рассматриваемому объекту источниками.
Для расчета индукции и напряженности магнитного поля, создаваемого электрическим током, используют закон Био - Савара -Лапласа
.
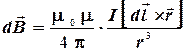Интегрируя данное соотношение, получаем выражение для магнитного поля в центре кругового тока
, (6.1)
а в любой точке на оси кругового тока на расстоянии l от центра
, (6.2)
где R - радиус витка; I - сила тока, протекающего по витку; m0 - магнитная постоянная, равная 4 p ×10-7 Гн/м (Генри/метр); m - магнитная проницаемость cреды. При l = 0 формула (6.2) переходит в формулу (6.1).
Если магнитное поле создано N1 близко расположенными другу к другу витками, то индукция соответственно увеличивается в N1 раз:
. (6.3)
При l = 0 
. (6.3,а)
Таким образом, для расчета индукции в заданной точке на оси кругового тока необходимо знать силу тока, текущего по витку, количество витков, радиус витка и расстояние от центра витка до заданной точки.
Если по витку течет постоянный ток, то и индукция в заданной точке остается постоянной. При пропускании переменного тока закон изменения индукции соответствует закону изменения тока. Если ток меняется по закону I = I0 sin w t, то при небольших w,когда можно пренебречь явлением самоиндукции, индукция магнитного поля меняется по закону
B = B0 sin w t, (6.4)
где В0 - максимальное значение модуля вектора магнитной индукции; w - циклическая частота (для промышленного тока n = 50 Гц, w = 2 p n = = 314 с-1).
Теория метода. Переменное магнитное поле может быть обнаружено с помощью флюксметра (от латинского flux - поток). Он состоит из небольшой проволочной катушки, соединенной с вольтметром. Для достаточно точного измерения значения индукции в определенной точке поля размеры катушки должны быть малы. При измерениях катушку флюксметра ориентируют так, чтобы ее сечение было перпендикулярно направлению вектора магнитной индукции.
В переменном магнитном поле в катушке наводится ЭДС индукции:
, (6.5)
где N2 - число витков катушки флюксметра, dФ / dt - скорость изменения магнитного потока, S2 - площадь сечения катушки флюксметра, a - угол между нормалью к сечению катушки и вектором магнитной индукции.
Из формулы (6.5) следует, что если силовые линии индукции магнитного поля перпендикулярны плоскости витков катушки флюксметра ( a = 0), то в катушке наводится ЭДС:
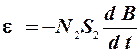(6.6)
или, учитывая формулу (6.4),
.
Амплитудное значение ЭДС e max определяется по формуле
e max = B0 N2 S2 w. (6.7)
При практическом применении формулы (6.7) необходимо помнить, что величина В0 – это не индукция магнитного поля в данной точке пространства при отсутствии флюксметра, а значение поля внутри флюксметра, которое существенно зависит от магнитной проницаемости сердечника флюксметра. В связи с этим представим соотношение (6.7) в виде:
B0 = С e max. (6.8)
Константа С, в дальнейшем называемая постоянной зонда, определяется числом витков флюксметра, площадью поперечного сечения, магнитной проницаемостью сердечника флюксметра и частотой изменения магнитного поля. Эту константу можно определить, если флюксметр поместить в такую точку пространства, для которой можно найти значение поля другим, независимым способом, например, в центр кругового витка. В этом случае можно воспользоваться выражением (6.3,а). Сравнивая соотношения (6.3,а) и (6.8), получаем
, (6.9)
где e0 – значение ЭДС флюксметра, находящегося в центре витка катушки, при заданном значении тока I0, протекающего внутри витков катушки.
Таким образом, максимальное значение индукции магнитного поля в любой точке пространства можно определить по формуле
, (6.10)
где e - эффективное значение ЭДС индукции флюксметра (оно меньше в 
его максимального значения e max). В центревитков значение e равно e0.
Порядок выполнения работы
1. Определить постоянную зонда.
1.1. Познакомиться с установкой и приборами. Определить цену деления амперметра и вольтметра, радиус катушки R.
|
1.2. Воспользовавшись омметром и микрометром рассчитать число витков N1 катушки. (В случае недостатка времени N1 должно быть задано).
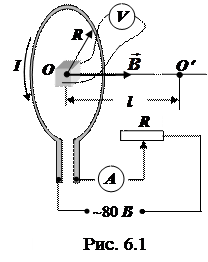
1.3. Собрать электрическую цепь кругового тока (рис 6.1).Зонд подключить к вольтметру (лучше к цифровому).
1.4.Напряжение ~80 В подать в цепь катушки, а 220 В - в цепь питания вольтметра. Зонд поместить в центр катушки.
1.5. С помощью реостата (или ЛАТРа) установить силу тока в катушке I0 = 0,5А. Поворачивая зонд вокруг вертикальной оси, добиться максимального значения индуцируемой ЭДС e0 (I0 и e0 записать в табл. 6.1).
Таблица 6.1
| d = r = N1 = R = á C ñ =Тл/В | |||||||
| I0,А | |||||||
| e0 ,В | |||||||
| С |
1.6. Уменьшая силу тока в катушке с шагом, равным ~0,05 А, измерения по п. 1.5 повторить 5-7 раз.
1.7. По каждой из пар I0 и e0 по формуле (6.9) вычислить постоянную зонда С. Найти ее среднее значение < С >.
2.Определить В0 в центре и в других точках на оси кругового тока.
2.1. По одному (лучше большему) из значений e0 (табл. 6.1) по формуле (6.10) вычислить В0 в центре кругового тока (катушки). Этот и последующие результаты занести в таблицу 6.2.
Таблица 6.2
| l,м | |||||||
| e,В | |||||||
| В0, Тл | |||||||
| В0, теор, Тл |
2.2. При силе тока I0, соответствующей выбранному в п. 2.1 e0, измерить ЭДС e (см. п. 1.5) в пяти - шести точках вдоль оси катушки (т.е. при разных l).
2.3. По полученным данным (табл. 6.2) вычислить В0 в этих точках.
2.4. Построить график зависимости В0 = f (l), где l - расстояние от данной точки до центра катушки. Сделать вывод.
2.5. Для тех же точек (тех же l) вычислить В0 = В0,теор по формуле
, при l = 0 
.
2.6. Полученные данные нанести на кривую (п. 2.4). Если будут расхождения с графиком, попробуйте найти этому объяснение.
3. Графически изобразить магнитное поле.
3.1. Укрепить на планшете лист бумаги.
3.2. Поместить зонд в произвольной точке сечения катушки (например, слева от центральной точки). Добиться максимального значения e. Отметить положение зонда точкой в вырезе площадки зонда.
3.3. Сдвинуть зонд так, чтобы его острие совпало с «меткой», сделанной в п. 3.2 и повторить п. 3.2 5 – 7 раз. Полученные точки плавно соединить, построив в результате силовую линию магнитного поля. Аналогично построить еще 2 – 4 силовые линии. Сделать вывод о структуре магнитного поля катушки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Магнитное поле. Основные характеристики магнитного поля. Единицы измерения.
2. Укажите способы получения магнитного поля.
3. Закон Био - Савара - Лапласа и его применение к расчету индукции магнитного поля тока.
4. Явление электромагнитной индукции. ЭДС индукции. Закон Фарадея.
5. Как вычислить индукцию магнитного поля в центре и на оси кругового тока?
6. Что такое линии индукции магнитного поля, для чего они нужны?
7. Что называется магнитным потоком через поверхность тела, какова единица его измерения?
8. Что такое эффективная сила тока и эффективное напряжение?
9. Сущность метода исследования магнитного поля с помощью флюксметра.
10. Порядок выполнения работы и ее результаты.
ЛАБОРАТОРНАЯ РАБОТА № 7
ОПРЕДЕЛЕНИЕ ИНДУКЦИИ
МАГНИТНОГО ПОЛЯ ЗЕМЛИ
