Решение дифференциальных уравнений с частными производными
Общие сведения
Дифференциальное уравнение с частными производными - это дифференциальное уравнение, содержащее несколько независимых переменных.
Порядок дифференциального уравнения с частными производными – наивысший порядок производной, входящей в дифференциальное уравнение.
Решением является функция, зависящая от нескольких аргументов.
Практическое применение такие уравнения нашли, например, при решении задач механики сплошных сред, в которых в качестве искомых функций обычно служат плотность, температура, напряжение и так далее. Аргументами этих функций являются координаты рассматриваемой точки в пространстве, а также время.
Математическая постановка задачи наряду с дифференциальным уравнением содержит также и некоторые дополнительные условия.
Если решение отыскивается в ограниченной области, то задаются условия на ее границе, называемые граничными (краевыми) условиями. Такие задачи называются краевыми.
Если одной из независимых переменных является время t, то задаются некоторые условия (например, значения искомых параметров) в начальный момент времени t0, называемые начальными условиями. Такие задачи называются задачами Коши. При этом задача решается в неограниченном пространстве, так как граничные условия не задаются.
Задачи, при формулировке которых ставятся и начальные и граничные условия, называются нестационарными ( или смешанными) краевыми задачами. Решения таких задач меняются с течением времени.
Рассмотрим виды дифференциальных уравнений с частными производными на примере дифференциального уравнения с частными производными второго порядка, линейного относительно производных, и двумя независимыми переменными x и y, общий вид которого
(9.1),
- где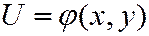 
- искомая функция,
- коэффициенты a, b, c, d, e, f, g, вообще говоря, могут зависеть от переменных х, у и искомой функции .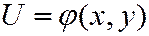
В связи с этим уравнение (9.1) может быть
1) с постоянными коэффициентами;
2) линейным, если функция g линейно зависит от U, а коэффициенты a, b, c, d, e, f зависят только от х, у;
3) квазилинейным, если коэффициенты a, b, c, d, e, f, g зависят от U.
В зависимости от соотношения коэффициентов уравнение (9.1) может быть:
1) уравнением первого порядка, которое называют уравнением переноса, если
a=b=c=f=0, d≠0, e≠0
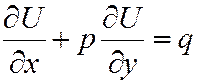(9.2)
Если в этом уравнении вместо х или у выступает время t, то тогда его называют эволюционным уравнением.
2) уравнением второго порядка, если хотя бы один из коэффициентов a, b, c отличен от 0. В зависимости от знака дискриминанта 
оно может принадлежать к одному из трех типов
- гиперболическому (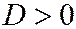
)
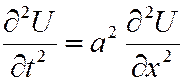- волновое уравнение (9.3)
- параболическому (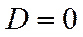
)
- уравнение теплопроводности или диффузии (9.4).
- эллиптическому (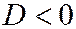
)
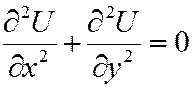
уравнение Лапласа (9.5).
Если в уравнении Лапласа правая часть отлична от 0, то оно называется уравнением Пуассона.
Приведенные уравнения называются уравнениями математической физики.
