 , (29)
, (29)
вид которой не меняется при изменении  .
.
Из уравнений (20) – (22) следует, что при очень коротких временах корреляции, когда  , T1=T2 и обратно пропорционально времени корреляции
, T1=T2 и обратно пропорционально времени корреляции 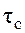 . Если время корреляции настолько мало, что
. Если время корреляции настолько мало, что 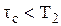 , то, как это следует из (21) и (22), T2 также обратно пропорционально
, то, как это следует из (21) и (22), T2 также обратно пропорционально 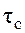 . Если же выполняется условие
. Если же выполняется условие  , то имеет место прямая пропорциональность T1 по отношению к
, то имеет место прямая пропорциональность T1 по отношению к 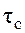 . Для логарифмов времен в одном случае имеем: lnT1, lnT2 ~ -ln
. Для логарифмов времен в одном случае имеем: lnT1, lnT2 ~ -ln 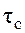 , а в другом lnT1~ln
, а в другом lnT1~ln 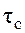 , вследствие чего графическое представление в двойной логарифмической системе координат для всех асимптот имеет линейную форму.
, вследствие чего графическое представление в двойной логарифмической системе координат для всех асимптот имеет линейную форму.
Время корреляции 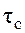 характеризует среднее время жизни молекулы в данном состоянии. Число молекул, обладающих достаточной энергией для преодоления потенциального барьера Ea, пропорционально
характеризует среднее время жизни молекулы в данном состоянии. Число молекул, обладающих достаточной энергией для преодоления потенциального барьера Ea, пропорционально  , поэтому для
, поэтому для 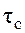 осуществляется температурная зависимость в виде уравнения Аррениуса
осуществляется температурная зависимость в виде уравнения Аррениуса
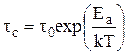 , (30)
, (30)
где  - постоянная.
- постоянная.
С учетом (30) на графике зависимости lnT1 и lnT2 от обратной температуры  , представленные асимптоты будут иметь наклон
, представленные асимптоты будут иметь наклон  , по которому можно определить высоту потенциального барьера Ea – энергию активации.
, по которому можно определить высоту потенциального барьера Ea – энергию активации.
Представление функций корреляции 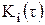 в виде простых экспонент с одним временем корреляции в полимерах является идеализированным упрощением. Можно представить себе, что только в направлении полимерной цепи в игру вступают различные времена корреляции. Поэтому функцию корреляции следует записывать в виде
в виде простых экспонент с одним временем корреляции в полимерах является идеализированным упрощением. Можно представить себе, что только в направлении полимерной цепи в игру вступают различные времена корреляции. Поэтому функцию корреляции следует записывать в виде
 , (31)
, (31)
где  – функция распределения времен корреляции. Учет распределения времен корреляции приводит к видоизменению выражений (20) – (22) для времен релаксации T1 и T2 и формы спада поперечной намагниченности (23):
– функция распределения времен корреляции. Учет распределения времен корреляции приводит к видоизменению выражений (20) – (22) для времен релаксации T1 и T2 и формы спада поперечной намагниченности (23):
 , (32)
, (32)
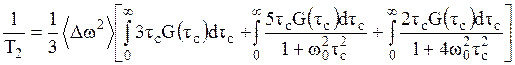 , (33)
, (33)
 , (34)
, (34)
 , (35)
, (35)
где A0 – начальное значение намагниченности. Описание данных по ядерной магнитной релаксации производят с помощью введения распределения времен корреляции в виде эмпирических функций гауссовой, логарифмически-гауссовой, Коула-Коула, Дэвидсона-Коула, Фуосса-Кирквуда той, или иной ширины. Часто удовлетворительных результатов достигают при введении спектра времен корреляции в форме функции Фуосса-Кирквуда, когда формулы (32), (34) и (35) переписываются в виде
 , (36)
, (36)
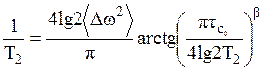 , (37)
, (37)
 , (38)
, (38)
где  – наивероятнейшее время корреляции,
– наивероятнейшее время корреляции, 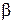 – параметр ширины распределения (
– параметр ширины распределения ( ). При β=0 распределение бесконечно широкое, а при β=1 – бесконечно узкое. Отметим, что когда
). При β=0 распределение бесконечно широкое, а при β=1 – бесконечно узкое. Отметим, что когда 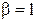 , спектр характеризуется одним временем корреляции и соотношения (36) – (38) совпадают с соотношениями, записанными ранее для экспоненциальной функции корреляции. Из (38) следует, что
, спектр характеризуется одним временем корреляции и соотношения (36) – (38) совпадают с соотношениями, записанными ранее для экспоненциальной функции корреляции. Из (38) следует, что
 . (38а)
. (38а)
Характерной особенностью наличия распределения Фуосса-Кирквуда является то, что при 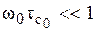 , как следует из (36),
, как следует из (36),  . То есть, имеет место дисперсия Т1 (зависимость от ω0), в противоположность случаю движения, описываемого одним временем корреляции, когда дисперсии Т1 нет. Кроме того, при выполнении этого же граничного условия (
. То есть, имеет место дисперсия Т1 (зависимость от ω0), в противоположность случаю движения, описываемого одним временем корреляции, когда дисперсии Т1 нет. Кроме того, при выполнении этого же граничного условия (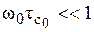 )
)  против
против  при описании движения одним временем корреляции.
при описании движения одним временем корреляции.
Из (37) при  следует, что
следует, что  , в то время как при отсутствии распределения времен корреляции
, в то время как при отсутствии распределения времен корреляции  .
.
Из (38) следует, что форма спада поперечной намагниченности является промежуточной между гауссовой, когда в показателе экспоненты (38) стоит t2, и экспоненциальной, когда в показателе экспоненты (38) стоит t.
Построение графиков зависимостей lnT1, lnT2 от обратной температуры также позволяет вычислить энергию активации. Однако теперь тангенс угла наклона графика  равен
равен  , а графика
, а графика 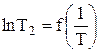 –
–  .
.
В современных спектрометрах предусмотрена возможность измерения времени спин-решеточной релаксации во вращающейся системе координат  и времени затухания намагниченности T2эфф при действии последовательности импульсов MW-4:
и времени затухания намагниченности T2эфф при действии последовательности импульсов MW-4:  . При движении с одним временем корреляции эти параметры описываются следующими выражениями
. При движении с одним временем корреляции эти параметры описываются следующими выражениями
 , (39)
, (39)
 . (40)
. (40)
где  ,
,  – напряженность магнитного поля спин-локинга.
– напряженность магнитного поля спин-локинга.
В условиях реального эксперимента  и
и  . Поэтому при
. Поэтому при 
вкладом двух последних слагаемых в (39) и (40) можно пренебречь. Тогда
 , (41)
, (41)
 . (42)
. (42)
Из (41) и (42) следует, что при  и
и 
 , а при
, а при  и
и 
 . Тангенс угла наклона зависимостей
. Тангенс угла наклона зависимостей  и
и  равен
равен  . Когда движение ядерных спинов описываются спектром времен корреляции в форме функции Фуосса-Кирквуда, то
. Когда движение ядерных спинов описываются спектром времен корреляции в форме функции Фуосса-Кирквуда, то  и T2эфф определяются соотношением
и T2эфф определяются соотношением
 , (43)
, (43)
 ,
, 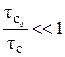 . (44)
. (44)
Из (43) и (44) следует, что при  и
и 
 и имеет место дисперсия
и имеет место дисперсия  и T2эфф, а именно
и T2эфф, а именно 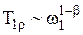 ,
,  . Тангенс угла наклона зависимостей
. Тангенс угла наклона зависимостей 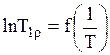 и
и  теперь равен
теперь равен  .
.






