Рассмотрим теперь поведение спиновой системы, подвергнутой воздействию одного или двух ВЧ-импульсов. Будем считать, что импульс включается и выключается так быстро, что огибающая ВЧ-колебаний во время импульса имеет прямоугольную форму. Примем также, что длительность импульса tp мала по сравнению с Т1 и Т2, так что релаксация за время tpне происходит.
Движение намагниченности ядер 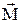 , определяемой как сумма магнитных моментов всех ядер
, определяемой как сумма магнитных моментов всех ядер  :
:
 , (2)
, (2)
в переменном магнитном поле ВЧ – импульса:
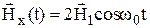 (3)
(3)
удобнее анализировать, если разложить поле на две составляющие с одинаковыми амплитудами Н1, одна из которых вращается в том же направлении, что и прецессирующие магнитные моменты ядер, другая – в противоположном направлении (рис. 2).

Рис. 2. Разложение линейно-поляризованного поля на две вращающиеся составляющие.
Обозначим эти вращающиеся составляющие через  и
и 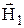 :
:
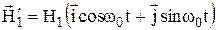 , (4)
, (4)
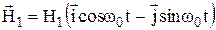 . (5)
. (5)
Здесь 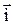 и
и  – единичные векторы вдоль осей Х и У соответственно. Вблизи резонанса составляющей
– единичные векторы вдоль осей Х и У соответственно. Вблизи резонанса составляющей  , вращающейся в противоположном направлении вполне можно пренебречь. Ниже мы будем пользоваться этим допущением.
, вращающейся в противоположном направлении вполне можно пренебречь. Ниже мы будем пользоваться этим допущением.
Теперь рассмотрим прямоугольную систему координат (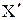 ,
, 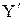 ,
,  ), вращающуюся вокруг поля H0 с частотой w0 в направлении, совпадающем с направлением прецессии вектора намагниченности
), вращающуюся вокруг поля H0 с частотой w0 в направлении, совпадающем с направлением прецессии вектора намагниченности 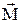 . Если направить поле
. Если направить поле 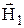 вдоль оси
вдоль оси 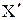 такой вращающейся системы координат (рис. 3), то под влиянием
такой вращающейся системы координат (рис. 3), то под влиянием 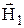 вектор
вектор 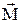 будет поворачиваться вокруг
будет поворачиваться вокруг 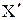 все время, пока действует поле
все время, пока действует поле 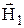 .
.
Другими словами, вектор 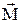 во вращающейся системе координат будет прецессировать вокруг
во вращающейся системе координат будет прецессировать вокруг 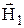 с угловой частотой w1 =gН1. Угол поворота вектора
с угловой частотой w1 =gН1. Угол поворота вектора 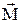 за время tp действия поля
за время tp действия поля 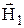 составит (в радианах) величину:
составит (в радианах) величину:
 , (6)
, (6)
Мы будем характеризовать импульсы как 90°-ный, когда q=p/2 и 180°-ый, когда q=p.

Рис. 3. Поведение вектора намагниченности 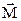 под действием переменного поля
под действием переменного поля  во вращающейся системе координат
во вращающейся системе координат






