Рассмотрим двухуровневую систему, содержащую Nядер со спином I= 1/2. Обозначим число спинов на нижнем уровне через N+,а на верхнем – N –. При этом очевидно, что N = N++ N –, а отношение населенностей уровней определяется фактором Больцмана
, (10)
где k— постоянная Больцмана и Т – абсолютная температура. Отметим, что в ядерном магнитном резонансе, за исключением самых низких температур (Т ~ 1К), всегда реализуется такая ситуация, при которой показатель степени в экспоненте 
очень мал, поэтому отношение N+/N – лишь незначительно отличается от единицы. Так, в поле 104 Э для протонов (максимальное 
) для температуры Т =300К величина 
. Отсюда, разложив экспоненту в ряд и ограничившись первыми двумя членами, можно записать:
. (10а)
Под воздействием переменного поля резонансной частоты будут происходить вынужденные переходы с нижнего уровня на верхний, соответствующие поглощению энергии высокочастотного поля, и обратные переходы, при каждом из которых выделяется квант энергии 
. При этом вероятности переходов в единицу времени – w(коэффициенты Эйнштейна) в обе стороны равны между собой. Несмотря на равенство вероятностей переходов вследствие малого, но конечного избытка спинов на нижнем уровне, число переходов снизу вверх в единицу времени будет превышать число переходов в обратном направлении, что приведет к поглощению энергии высокочастотного поля и постепенному выравниванию населенностей.
Если ввести величину n– разность населенностей уровней
, (11)
то, записав дифференциальные уравнения для изменения населенностей уровней N+ и N –- со временем
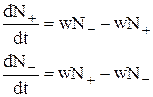, (12)
можно найти
. (13)
Решение уравнения (13) имеет вид
, (14)
где n(0) – значение nпри t = 0. Из (14) видно, что если вначале населенности уровней были различными, то под воздействием переменного поля с течением времени nстремится к нулю, что должно приводить к прекращению поглощения энергии высокочастотного поля – насыщению.
Насыщению противодействует взаимодействие системы спинов с решеткой, под которой обычно понимается вещество, содержащее резонирующие ядра, независимо от того, является ли оно твердым телом, жидкостью или даже газом. В результате этого взаимодействия, в частности, устанавливается больцмановское отношение населенностей уровней (10) при помещении системы спинов в постоянное магнитное поле, когда переменное поле отсутствует. Нетрудно видеть, что это имеет место только в том случае, если вероятность переходов под воздействием спин-решеточного взаимодействия сверху вниз 
будет больше вероятности обратного перехода 
. Действительно, в стационарном состоянии изменение числа частиц, например на нижнем уровне
, (15)
должно равняться нулю, откуда следует, что
. (16)
Тогда с учётом (10) получим
. (17)
Записав теперь выражение
(18)
и используя (11) и (15), найдём дифференциальное уравнение для n
. (19)
Если ввести среднюю вероятность перехода 
, то, используя (17), можно найти 
и 
, после чего уравнение (19) преобразуется к виду
, (20)
где введены обозначения: 
; 
; n0 соответствует равновесной разности населённостей, которая устанавливается при термодинамическом равновесии системы спинов с решёткой при отсутствии переменного поля. Интегрирование выражения (20) даёт
, (21)
где А – постоянная интегрирования. Если в образце при t=0 спины не были ориентированы (n=0), то A=–n0, поэтому возрастание намагниченности первоначально ненамагниченного образца происходит по закону
(21а)
Видно, что величина Т1, имеющая размерность времени, характеризует скорость установления разности населенностей уровней за счет спин-решеточного взаимодействия. Она носит название времени спин-решеточной релаксации.
В реальных условиях эксперимента под влиянием двух конкурирующих процессов – насыщения под действием переменного поля, стремящегося уменьшить разность населенностей до нуля, и спин-решеточной релаксации, ведущей к равновесной разности населенностей n0,устанавливается квазиравновесное распределение спинов по уровням, характеризуемое числом n. Объединяя уравнения (13) и (20), запишем для него дифференциальное уравнение в виде
. (22)
С установлением квазиравновесия 
, откуда можно найти
. (23)
Если 
, то n почти не отличается от равновесной величины n0. Поскольку w пропорционально квадрату амплитуды высокочастотного поля [1], это условие выполняется для малых полей или быстрых релаксационных процессов (малое T1). С ростом амплитуды переменного поля, когда 
становится порядка единицы, n начинает заметно падать. При дальнейшем увеличении поля скорость поглощения энергии стремится к постоянной величине
. (24)
Однако результирующий сигнал, который мы наблюдаем в эксперименте по ЯМР, пропорционален не поглощённой мощности, а избытку населенности на нижнем уровне – n [2]. Поэтому, как это следует из (23), при неограниченном росте напряжённости радиочастотного поля значение n и, следовательно, полезный сигнал, будут уменьшаться до нуля.
