Многие ядра обладают отличным от нуля механическим моментом количества движения 
. Такие ядра имеют также и магнитный момент 
.При этом векторы и параллельны и, следовательно
, (1)
где 
– скалярная величина, называемая гиромагнитным отношением. В квантовой механике – оператор 
, который связан с оператором спина 
соотношением
, (2)
где 
– приведенная постоянная Планка. Оператор 
имеет собственные значения I(I + 1), где I–спиновое число или просто спин.
В магнитном поле 
магнитный момент обладает энергией 
, которая называется зеемановской. Ей соответствует зеемановский гамильтониан
. (3)
В случае постоянного магнитного поля H, которое будем считать направленным по оси z, 
можно записать в виде
, (4)
где 
– оператор z-проекции спина, Н0=Нz. может принимать одно из (2I+1) собственных значений
m=I, I–1,…,–I, (5)
поэтому соответствующие гамильтониану (4) возможные значения энергии равны
. (6)
На рис. 1 изображены схемы уровней энергии ядер для I=1/2(a) и I=1(б). Для двухуровневой системы m=+1/2 соответствует максимальной проекции спина и магнитного момента, ориентированного по направлению поля H0, а m=–1/2 – против поля. Разность энергии 
соседних уровней (
), как это следует из выражения (6), для любого I равна
. (7)
Рис. 1. Уровни энергии ядер в магнитном поле: а – 
, б –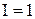 
Если систему невзаимодействующих магнитных ядер, помещенных в постоянное магнитное поле, подвергнуть облучению высокочастотным (радиочастотным) полем с частотой 
, кванты энергии которого совпадают с , т.е.
, (8)
где 
– угловая частота, то это поле будет вызывать резонансные переходы между уровнями. В соответствии с квантовомеханическими правилами отбора переходы возможны только между соседними уровнями, т. е. при , и в этом случае, согласно (8), резонансная частота равна
. (9)
