На раскрой (распил, обработку) поступает материал одного образца в количестве A единиц. Требуется изготовить из него m разных комплектующих изделий в количествах, пропорциональных числам bi (i = 1,…, m) – условие комплектности.
Каждая единица материала может быть раскроена n различными способами, причем использование j-го способа (j = 1,…, n) дает aij единиц i-го изделия (i = 1,…, m).
Необходимо найти план раскроя, обеспечивающее максимальное количество комплектов.
Обозначим xj – число единиц материала, раскраиваемых j-ым способом,
x – число изготавливаемых комплектов изделий.
Так как общее количество материала равно сумме его единиц, раскраиваемых различными способами, то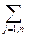 
xj = A.
Требование комплектности выразится уравнениями
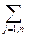xjּaij = biּx (i = 1,…, m)
Кроме того xj ≥ 0 (j = 1,…, n).
Практический блок
Пример
Составить математическую модель задачи линейного программирования и найти решение геометрическим способом.
1. По данным, приведенным в таблице 2.2.3 составить систему математических зависимостей (неравенств) и целевую функцию.
2. Изобразить геометрическую интерпретацию задачи и найти оптимальное решение.
3. Провести аналитическую проверку и определить значение целевой функции.
4. Определить избытки ресурсов.
5. Вычислить объективно обусловленные оценки.
6. Исследовать устойчивость решения.
Таблица 2.2.3 – Матрица удельных нормативов.
| Продукция | Сырье | Прибыль на одно изделие | ||
| Рес. 1 | Рес. 2 | Рес. 3 | ||
| I. Изделие 1 | 2.4 | 8.0 | 6.2 | 50 ( )
|
| II. Изделие 2 | 12.2 | 5.4 | 2.2 | 40 ( )
|
| Наличие ресурсов | – |
Решение:
1. Обозначим:
– объем изделия 1;
– объем изделия 2.
Опишем модель с помощью системы неравенств линейных уравнений:
;
;
;
;
– целевая функция (критерий оптимальности).
