Предприятию задан план производства m видов продукции по времени и номенклатуре: требуется за время Т выпустить bi (i=1,…,m) единиц продукции каждого типа. Продукция производится на станках n типов. Для каждого станка известны производительность aij (то есть, количество продукции j-го вида, которое можно произвести на станке i-го типа) и затраты cij на изготовление продукции j-го вида на станке i-го типа в единицу времени.
Необходимо составить такой план работы станков (т.е. так распределить выпуск продукции между станками), чтобы затраты на производство всей продукции были минимальными.
Обозначим xij – время, в течение которого станок i-го типа будет занят изготовлением продукции j-го вида (i = 1,…, m; j = 1,…, n).
Затраты на производство всей продукции выразятся функцией F = 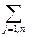
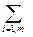 cijּxij, которую нужно минимизировать.
cijּxij, которую нужно минимизировать.
Для выполнения плана выпуска по номенклатуре необходимо, чтобы выполнялись следующие равенства: 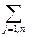 aijּxij = bi (i=1,…, n).
aijּxij = bi (i=1,…, n).
Кроме того, xij ≥ 0 (i = 1,…,m; j = 1,…, n).
Так как время работы каждого станка ограничено и не превышает Т, то система ограничений может быть дополнена неравенствами:
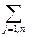 xij ≤ T (i = 1,…, n).
xij ≤ T (i = 1,…, n).






