Дневная диета должна содержать m видов различных питательных веществ, соответственно, в количестве не менее bi (i = 1,…, m) единиц. Имеется n различных продуктов в количестве dj (j=1,…, n) единиц.
 Пусть аij – количество единиц i-го питательного вещества, содержащегося в единице j-го продукта; cj – стоимость единицы j-го продукта.
Пусть аij – количество единиц i-го питательного вещества, содержащегося в единице j-го продукта; cj – стоимость единицы j-го продукта.
Определить, какие продукты и в каком количестве необходимо включить в диету, чтобы она удовлетворяла минимальной дневной потребности в каждом питательном веществе при наименьшей общей стоимости используемых продуктов.
Обозначим через хj (j = 1,…, n) количество единиц j-го продукта в диете; тогда задача имеет следующую математическую модель.
Найти минимальное значение линейной функции F = 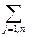 (cj•xj)
(cj•xj)
при ограничениях 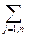 (aij•xj) ≥ bi, i = 1,…, m (2.2.14)
(aij•xj) ≥ bi, i = 1,…, m (2.2.14)
0 ≤ xj ≤ dj, j = 1,…, n
К этому виду задач относятся также задачи составления дневного рациона, задачи на составление смесей, а также некоторые задачи планирования производства.






