

|
| Продолжение |
Значения параметров модели  могут
могут

|

|
быть определены двумя способами. Согласно первому способу полученные значения параметров потока отказов автомобиля, связанных с его текущим ремонтом, капитальным ремонтом и списанием его агрегатов, аппроксимируются экспоненциальными зависимостями следующего вида:
Ошибка аппроксимации при небольших п бывает высокой и может достигать 10—20%. Это один из главных недостатков первого способа, существенно снижающий точность последующих расчетов годового пробега. Указанный недостаток можно исключить.
Согласно второму способу параметры  задаются дис-
задаются дис-
кретно для каждого интервала пробега и являются постоянными величинами на каждом заданном интервале пробега, составляющем 10—20 тыс. км, но значения этих параметров меняются в течение пробега с начала эксплуатации автомобиля скачкообразно от одного интервала к другому.
Метод динамики средних может быть использован и для определения коэффициента выпуска автопарка, состоящего из автомобилей разных моделей.
Указанная задача может быть решена двумя способами. Первый способ состоит в рассмотрении изолированного процесса эксплуатации совокупности автомобилей одной модели.
Второй способ предполагает рассмотрение процесса функционирования моделей автомобилей многомарочного парка в целом. В этом случае без принципиальных изменений может быть использован изложенный выше способ, разница будет только в том, что
число дифференциальных уравнений увеличится в п раз, где п — число моделей подвижного состава, обслуживаемых на одних и тех же постах ТО и ТР. Использование метода динамики средних для определения коэффициентов технической готовности и выпуска автомобилей моделей разномарочного парка1 позволяет учесть ограниченное количество постов для проведения ТО и ТР.
При определении коэффициентов технической готовности и выпуска автомобилей разномарочного парка необходимо разбить все модели подвижного состава, эксплуатирующегося в АТП, на группы, включающие автомобили тех моделей, которые обслуживаются на одних и тех же постах ТО-2 и ТР. Для каждой группы моделей подвижного состава строится единая система дифференциальных уравнений, описывающая функционирование соответствующей группы автомобилей1.
Задачи
2.1. В моменты времени  проводится осмотр ЭВМ. Воз-
проводится осмотр ЭВМ. Воз-
можны следующие состояния ЭВМ:
 — полностью исправна;
— полностью исправна;
 — незначительные неисправности, которые позволяют экс
— незначительные неисправности, которые позволяют экс
плуатировать ЭВМ;
 — существенные неисправности, дающие возможность ре
— существенные неисправности, дающие возможность ре
шать ограниченное число задач;
 — ЭВМ полностью вышла из строя.
— ЭВМ полностью вышла из строя.
Матрица переходных вероятностей имеет вид

Постройте граф состояний. Найдите вероятности состояний ЭВМ после одного, двух, трех осмотров, если вначале 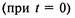 ЭВМ была полностью исправна.
ЭВМ была полностью исправна.
2.2. Магазин продает две марки автомобилей А и В. Опыт эксплуатации этих марок автомобилей свидетельствует о том, что для
них имеют место различные матрицы переходных вероятностей, соответствующие состояниям: работает хорошо (состояние 1) и требует ремонта (состояние 2):

Элементы матрицы перехода определены на годовой период эксплуатации автомобиля. Требуется:
1) найти вероятности состояний для каждой марки автомобиля после двухлетней эксплуатации, если в начальном состоянии автомобиль «работает хорошо»;
2) определить марку автомобиля, являющуюся более предпочтительной для приобретения в личное пользование.
2.3. Система ^-автомобиль может находиться в одном из пяти
возможных состояний:
исправен, работает;
неисправен, ожидает осмотра;
осматривается;
ремонтируется;
списывается.
Постройте граф состояний системы.
2.4. Организация по прокату автомобилей в городе выдает ав
томобили напрокат в трех пунктах города: А, В, С. Клиенты могут
возвращать автомобили в любой из трех пунктов. Анализ процесса
возвращения автомобилей из проката в течение года показал, что
клиенты возвращают автомобили в пункты А, В, С в соответствии
со следующими вероятностями:

Требуется:
1) в предположении, что число клиентов в городе не изменяется, найти процентное распределение клиентов, возвращающих автомобили по станциям проката к концу года, если в начале года оно было равномерным;
2) найти вероятности состояний в установившемся режиме;
3) определить пункт проката, у которого более целесообразно строить станцию по ремонту автомобилей.
2.5. Рассматривается процесс накопления терминов в динами
ческом словаре (тезаурусе) при функционировании автоматизиро
ванного банка данных (АБД). Сущность процесса в том, что терми
ны заносятся в словарь по мере их появления в той информации,
которая вводится в АБД. Например, в АБД автоматизированной
системы управления производством (АСУП) могут в качестве тер
минов заноситься наименования организаций, с которыми данное
предприятие поддерживает производственные отношения. Дина
мический словарь наименрваний таких организаций будет накап
ливаться в АБД АСУП по мере появления этих наименований в
единицах информации, вводимых в АБД.
В каждой единице информации, поступающей в АБД, в среднем встречается х терминов словаря, а интенсивность поступления единиц информации в АБД равна  Следовательно, интенсивность потока терминов словаря в информации, поступающей в АБД, будет
Следовательно, интенсивность потока терминов словаря в информации, поступающей в АБД, будет  Предполагается, что поток терминов словаря является пуассоновским. Число терминов словаря п является конечным и неслучайным, хотя, возможно, и неизвестным нам заранее. Все термины словаря могут находиться в единице информации с одинаковой вероятностью. В словарь заносятся, естественно, лишь те термины, которые до сих пор еще не встречались в единицах информации.
Предполагается, что поток терминов словаря является пуассоновским. Число терминов словаря п является конечным и неслучайным, хотя, возможно, и неизвестным нам заранее. Все термины словаря могут находиться в единице информации с одинаковой вероятностью. В словарь заносятся, естественно, лишь те термины, которые до сих пор еще не встречались в единицах информации.
Требуется найти математическое ожидание и дисперсию числа терминов, накопленных в динамическом словаре1.
2.6. Водитель такси обнаружил, что если он находится в городе
А, то в среднем в 8 случаях из 10 он везет следующего пассажира в
город Б, в остальных случаях будет поездка по городу А. Если же
он находится в городе Б, то в среднем в 4 случаях из 10 он везет
следующего пассажира в город А, в остальных же случаях будет по
ездка по городу Б.
Требуется:
1) перечислить возможные состояния процесса и построить граф состояний;
2) записать матрицу переходных вероятностей;
3) найти вероятности состояний после двух шагов процесса, если:
а) в начальном состоянии водитель находится в городе А;
б) в начальном состоянии водитель находится в городе Б;
4) найти вероятности состояний в установившемся режиме.
2.7. Система S представляет собой техническое устройство, со
стоящее из т узлов и время от времени (в моменты tb t2i..., tk) под
вергающееся профилактическому осмотру и ремонту. После каждо
го шага (момента осмотра и ремонта) система может оказаться в
одном из следующих состояний:
 — все узлы исправны (ни один не заменялся новым);
— все узлы исправны (ни один не заменялся новым);
 — один узел заменен новым, остальные исправны;
— один узел заменен новым, остальные исправны;
 _ — два узла заменены новыми, остальные исправны;
_ — два узла заменены новыми, остальные исправны;
 9 — i узлов (/ < т) заменены новыми, остальные исправны;
9 — i узлов (/ < т) заменены новыми, остальные исправны;
 , — все т узлов заменены новыми. Суммарный поток моментов окончания осмотров для всех узлов — пуассоновский с интенсивностью X = 4. Вероятность того, что
, — все т узлов заменены новыми. Суммарный поток моментов окончания осмотров для всех узлов — пуассоновский с интенсивностью X = 4. Вероятность того, что  в момент профилактики узел придется заменить новым, равна
в момент профилактики узел придется заменить новым, равна
Рассматривая процесс профилактического осмотра и ремонта (замены) как марковский процесс размножения, вычислите вероятности состояний системы (S) в стационарном режиме (для т = 3), если в начальный момент времени все узлы исправны1.
2.8. Техническое устройство имеет два возможных состояния:
 — исправно, работает;
— исправно, работает;
 — неисправно, ремонтируется.
— неисправно, ремонтируется.
Матрица переходных вероятностей имеет вид:

Постройте граф состояний. Найдите вероятности состояний после третьего шага и в установившемся режиме, если в начальном состоянии техническое устройство исправно.
2.9. Система S состоит из двух узлов — I и II, каждый из кото
рых может в ходе работы системы отказать (выйти из строя).
Перечислите возможные состояния системы и постройте граф состояний для двух случаев:
1) ремонт узлов в процессе работы системы не производится (чистый процесс гибели системы);
2) отказавший узел немедленно начинает восстанавливаться.
2.10. В городе издаются три журнала: Q, С2, С3, и читатели вы
писывают только один из них. Пусть в среднем читатели стремят
ся поменять журнал, т. е. подписаться на другой не более одного
раза в год, и вероятности таких изменений постоянны. Результаты
маркетинговых исследований спроса читателей на журналы дали
следующее процентное соотношение:
80% читателей Сх подписываются на С2; 15% читателей С2 подписываются на С3; 8% читателей С3 подписываются на Cj. Требуется:
1) записать матрицу переходных вероятностей для средних годовых изменений;
2) предположить, что общее число подписчиков в городе постоянно, и определить, какая доля из их числа будет подписываться на указанные журналы через два года, если по состоянию на 1 января текущего года каждый журнал имел одинаковое число подписчиков;






