Решение. 1. Граф состояний показан на рис

1. Граф состояний показан на рис. 2.10, в котором

— все четыре НМД нуждаются в профилактическом ремонте;

— один НМД успешно прошел профилактику, а три НМД
нуждаются в профилактическом ремонте;

— два НМД успешно прошли профилактику, а два нуждают­
ся в профилактическом ремонте;

— три НМД успешно прошли профилактику, один нуждает­
ся в профилактическом ремонте;

— все четыре НМД успешно прошли профилактику.

 

Рис. 2.10. Граф состояний системы

Каждый профилактический ремонт успешно заканчивается с вероятностью р, что равносильно /^-преобразованию потока окон­чаний ремонтов, после которого он остается пуассоновским, но с интенсивностью pk(f). В этом примере мы имеем дело с процессом чистого размножения с ограниченным числом состояний.

2. Уравнения Колмогорова имеют следующий вид:

 

(2.25)

 

 

Начальные условия При по-

стоянной интенсивности и вероятности состояний опреде-

ляются по следующим формулам:

 

(2.26)

 

3. Математическое ожидание числа дисков, успешно прошед­ших профилактику к моменту равно:

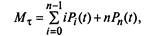
(2.27)

Пример 2.6. Рассмотрим производство автомобилей на заводе. Поток производимых автомобилей — нестационарный пуассонов-ский с интенсивностью . Найдем одномерный закон распределе­ния случайного процесса — число выпущенных автомобилей к моменту времени /, если в момент начат выпуск автомобилей.