Моделирование работы подвижного состава с использованием марковских случайных процессов

Представим автомобиль как некоторую систему 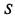с дискретны­ми состояниями которая переходит из состояния в состояние под влиянием случайных событий (отказов).

На стадии прогнозирования (планирования) работы автомоби­ля целесообразно рассматривать следующие состояния, в которых подвижной состав может находиться в процессе эксплуатации и котооые характеризуются целодневными простоями:

— исправен, работает;

— находится на капитальном ремонте (КР);

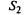— проходит ;

— находится в текущем ремонте (ТР);

— исправен, не работает по организационным причинам (без
водителя, шин, запасных частей);

— не работает, снятие агрегата для отправки на капитальный
ремонт;

— не работает, списание агрегата, замена на новый;

— исправен, не работает (выходные и праздничные дни);

— списывается.

Надо отметить, что в настоящее время вышеперечисленные со­стояния автомобиля планируются при разработке годовой програм­мы работы автотранспортного предприятия (АТП), при этом состо­яния объединяются в одно состояние «находится в ТР».

Для анализа процесса эксплуатации автомобиля как случайно­го процесса с дискретными состояниями удобно воспользоваться геометрической схемой, так называемым графом состояний (рис. 2.12). Граф состояний изображает возможные состояния авто­мобиля и его возможные переходы из состояния в состояние.

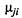На рис. 2.12 через и обозначены плотности вероятнос­тей перехода автомобиля из состояния 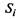в состояние Напри-

 

Рис. 2.12. Граф состояний автомобиля

мер, — плотность вероятности перехода автомобиля из состо­яния «исправен, работает» в состояние «находится в текущем ре­монте».

Можно считать, что события, переводящие автомобиль из со­стояния в состояние, представляют собой потоки событий (напри­мер, потоки отказов). Если все потоки событий, переводящие сис­тему (автомобиль) из состояния в состояние, пуассоновские (ста­ционарные или нестационарные), то процесс, протекающий в сис­теме, будет марковским, а плотности вероятности перехода 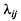в непрерывной цепи Маркова представляют собой интенсивности потока событий, переводящего систему из состояния в состоя­ние . Например, — интенсивность потока отказов автомоби­ля, который переводит автомобиль из состояния «исправен, рабо­тает» в состояние «находится в ТР».

Рассматриваемые состояния автомобиля характеризуются средним числом дней пребывания автомобиля в каждом состоянии . Показатели находят отражение в статистической отчетно­сти автотранспортного предприятия. Отношение

(2.28)

где — число календарных дней в году.

можно трактовать как вероятность нахождения автомобиля в -м состоянии.

Вероятности состояний автомобиля как

функции пробега в случае марковского процесса с дискретными состояниями и непрерывным временем удовлетворяют определен­ного вида дифференциальным уравнениям (уравнениям Колмого­рова), записываемым в виде

 

Число уравнений в системе (2.29) зависит от числа состояний автомобиля. Вероятность нахождения автомобиля в состоянии «ис-правен-работает» представляет собой коэффициент выпуска

а сумма вероятностей - коэф-

фициент технической готовности автомобиля.

Поскольку большинство интенсивностей перехода зависят от пробега, то решение системы (2.29) производится с помощью ме­тодов численного интегрирования, например метода Рунге-Кутта.

Необходимо учесть, что для расчета производственной програм­мы АТП требуется зачастую определять показатели работы группы автомобилей определенной модели у-го возраста (коэффициент вы­пуска и годовой пробег автомобиля у-й возрастной группы).

Для описания процесса функционирования группы автомоби­лей может быть использован метод динамики средних. Этот метод вытекает из теории марковских случайных процессов. Удобство его заключается в том, что, зная возможные состояния одного (услов­ного) автомобиля, можно моделировать процесс функционирова­ния группы из любого числа автомобилей.

Схема, изображающая процесс работы условного автомобиля определенной модели, аналогична схеме рис. 2.12, лишь с той раз­ницей, что через и обозначены средние интенсивности потоков событий, переводящих автомобиль из состояния S; в состояние Sp и наоборот. При этом каждое состояние характеризуется средней численностью автомобилей Nj(t), находящихся в нем в момент вре­мени t. Очевидно, что для любого / сумма численностей всех состо­яний равна общей численности автомобилей исследуемой группы:

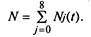
Величина для любого / представляет собой случайную ве-

личину, а при меняющемся / — случайную функцию времени.

Зная граф состояний (рис. 2.12) и соответствующие интенсив­ности перехода Х_/7 и jli_/7, определим средние численности автомоби­лей как функции пробега

Согласно графу состояний (рис. 2.12) система дифференциаль­ных уравнений для средних численностей состояний запишется следующим образом:

 

 

 

(2.30)

Отношение равно коэффициенту выпуска автомоби-

лей определенной модели на пробеге L с начала их эксплуатации, а отношение — коэффициенту техниче-

ской готовности автомобилей.

Докажем, что формулы для определения коэффициентов техни­ческой готовности (к_тг), выпуска подвижного состава (ос_в) являются частным случаем, соответствующим стационарному решению систе­мы уравнений (2.30), описывающей функционирование автопарка.

Для расчета средней численности автомобилей, находящихся в исправном состоянии, можно предварительно объединить состояния в одно состояние: «исправен» — Тогда граф состояний условного автомобиля примет вид, представленный на рис. 2.13.

 

Рис. 2.13. Граф состояний условного автомобиля

Система дифференциальных уравнений для средних численно-стей подвижного состава запишется следующим образом:

(2.31)

 

Положим левые части уравнений равными нулю, получим сис­тему алгебраических уравнений для средних численностей состоя­ний автопарка, работающего в стационарном режиме:

 

Решим систему алгебраических уравнений с учетом так называ­емого нормировочного условия:

где , - среднесписочная численность автопарка, шт.

Для примера из системы (2.32) определим неизвестные средние численности состояний, используя N{. Так, из второго и третьего уравнений имеем

 

Согласно нормировочному условию

 

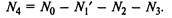
Подставляя в первое уравнение (2.32), получим:

 

Разделим полученное уравнение на jn^:

 

Последнее уравнение можно записать следующим образом:

 

Тогда коэффициент технической готовности равен:

(2.37)

Интенсивности перехода автомобиля в состояния «тех­ническое обслуживание», «текущий ремонт», «капиталь­ный ремонт» соответственно, отк/тыс. км; интенсивности восстановления, равные обратным сред­ним величинам продолжительности соответствующих ремонтных воздействий технического обслуживания (ТО-2), текущего ремонта (ТР), капитального ремонта (КР), отк/день.