Уравнение линейной зависимости сопротивления от температуры: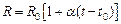 
, где 
- сопротивление при начальной температуре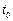 
; 
- увеличение температуры внутри интервала; 
- температурный коэффициент сопротивления. Если его переписать в виде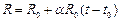 
, это уравнение становится похоже на уравнение линейной зависимости 
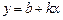, где 
имеет смысл отсекаемого ординатного отрезка;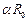 
- углового коэффициента прямой, 
; 
.
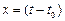Параметры эмпирической формулы 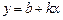вычисляют по методу наименьших квадратов с охватом всех n экспериментальных точек с координатами 
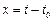, при этом значение 
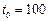°С. Основная задача метода наименьших квадратов: вычислить такие значения параметров 
и 
эмпирической формулы, чтобы сумма 
квадратов ординатных отклонений эмпирической прямой была минимальной:
.
Из условий минимума функции двух переменных: 
, 
получают формулы метода наименьших квадратов:
,
.
Для расчётов и составляют таблицу:
| Номер измерений | 
|
| 
| 
|
| ... | ||||
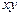
| n = |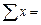 
| 
| 
| 
|
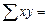
При нахождении сумм не следует делать округлений. Затем вычисляют и , а также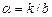 
и записывают эмпирическую формулу с числовыми значениями входящих в нее величин.
Вычисленный температурный коэффициент сравнивают с табличным значением для меди. Для анализа качества эмпирической формулы вычисляют разности между измеренными и расчетными значениями сопротивлений во всех точках графика и анализируют эти отличия.
Если эмпирическая формула доброкачественная, то по величине сопротивления проволоки можно вычислить ее температуру, т.е. пользоваться электрическим термометром сопротивления, имеющим целый ряд преимуществ перед обычным ртутным термометром.
