Классическая электронная теория проводимости металлов, в которой впервые были теоретически получены известные из опыта законы Ома и Джоуля - Ленца не является исчерпывающей. Одно из затруднений этой теории - неудача с получением известной из опыта линейной зависимости удельного электрического сопротивления от температуры: ρ ~ T. По классической теории 
, где m,e - масса и заряд электрона, n 0 - концентрация свободных электронов в единице объема металла, u - средняя скорость теплового движения свободных электронов, λ - средняя длина свободного пробега электрона между соударениями с атомами кристаллической решетки металла. От температуры существенно зависит только скорость u. Из следствий молекулярно-кинетической теории газов 
следует, что 
. Значит, по классической теории получается. что 
а это противоречит опытным данным, так как 
. Затруднения классической теории вызваны тем, что электроны, как объекты физического микромира, не подчиняются в полной мере законам классической физики макромира.
Правильно объясняет влияние температуры на электрическое сопротивление квантово механическая теория, учитывающая волновые свойства электронов как микрочастиц. По квантовой теории сопротивление возникает за счет рассеяния электронных волн на тепловых колебаниях решетки. При этом от температуры существенно зависит длина свободного пробега (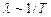
). Скорость электронов от температуры практически не зависит в силу так называемого вырождения электронного газа. По квантовой теории , что согласуется с опытными данными.
Линейная зависимость сопротивления от температуры несколько приближенная, потому что кроме рассеяния электронных волн на тепловых колебаниях решетки имеется еще рассеяние на примесных атомах в решетке, на искажениях решетки. Поэтому линейное уравнение составляют для некоторого температурного интервала, причем для составления уравнения используется много экспериментальных точек.
