1. Электрическая лампочка нагревателя и блок питания моста работают от сетевого напряжения 220 В.
2. Температура разогрева термометра достигает 180 °С, поэтому не следует касаться экранов, закрывающих электролампу.
3. Следует лишь на короткое время включать кнопкой гальванометр, когда мост Уитстона не уравновешен.
Содержание отчета
1. Название работы.
2. Цель работы (техническое задание).
3. Краткие сведения о классической и квантовой теории проводимости металлов.
4. Схема установки со спецификацией.
5. Таблица и график результатов измерений.
6. Таблица и расчеты по методу наименьших квадратов.
7. Полученная эмпирическая формула.
8. Сравнение полученного значения температурного коэффициента сопротивления с табличным значением для меди.
9. Анализ качества полученной эмпирической формулы.
Вопросы для допускного контроля
1. Чем обусловлена высокая электрическая проводимость металлов?
а) наличием в металле свободных электронов,
б) малым электрическим сопротивлением,
в) большой скоростью движения электронов в металле,
г) высокой концентрацией свободных электронов в металле.
2. При нагревании сопротивление у металлов...у электрических растворов...:
а) мало изменяется; сильно изменяется;
б) понижается; понижается,
в) увеличивается; уменьшается;
г) растет; растет.
3. Полученное значение коэффициента 
К-1, а табличное 
К-1. Каково отличие в процентах?
а) 1,05; б) 10; в) 5; г) 0,18.
4. Получены экспериментальные точк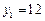и: 
, 
и 
, 
. Чему равен коэффициент 
рассчитанный по формуле метода наименьших квадратов в формуле эмпирической линейной зависимости 
от 
?
а) 0,3; б) 9; в) 90; г) 0,033.
Контрольные вопросы
1. Как записываются и формулируются законы Ома и Джоуля-Ленца в дифференциальной форме? Как они выводятся?
2. Как выводится закон Ома в классической электронной теории проводимости металлов?
3. В каких технических устройствах используется зависимость электрического сопротивления материала от температуры?
4. Чему равна "цена деления" исследованного в работе термометра сопротивления? Какое минимальное изменение температуры можно им обнаружить?
5. Осуществите вывод формул метода наименьших квадратов, используя имеющиеся в данной работе указания.
