Теория метода. Для решения простейших задач расчета сил токов, сопротивлений, напряжений используют закон Ома

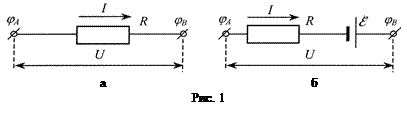
Для решения простейших задач расчета сил токов, сопротивлений, напряжений используют закон Ома. Закон Ома для замкнутой цепи (контура) , для одно­родного участка цепи (рис. 1а), в случае неоднородного участка цепи, т.е. содержащего источник ЭДС, (рис. 1б) яв­ляется обобщенным законом Ома и имеет вид: .

Для решения более сложных задач при расчете разветвленных электриче­ских цепей используют два закона Кирхгофа.

Первый закон Кирхгофа справедлив для любого узла слож­ной электрической цепи. В узле электрической цепи сходятся не менее трех проводников, трех токов. Первый закон Кирхгофа являет­ся следствием одного из главных законов природы - закона со­хранения электрического заряда. Поскольку ток - это перенос зарядов, сумма токов, входящих в узел, должна равняться сумме токов, выходящих из узла. Первый закон Кирхгофа формулирует­ся следующим образом: алгебраическая сумма токов сходящихся в узле равна нулю

,

при этом входящим токам приписывают знак плюс, выходящим - знак минус.

Второй закон Кирхгофа справедлив для каждого замкнутого контура из числа тех, которые можно мысленно выделить в сложной электрической цепи. Каждая "сторона" контура в общем случае представляет собой неоднородный, содержащий R и E участок цепи. Но среди сторон могут быть и однородные, т.е. со­держащие только R, участки цепи. Допустим, что выделили замк­нутый контур АВСА с тремя "сторонами", содержащими, соот­ветственно R ₁, E ₁, R ₂, E ₂, R ₃, E ₃. На основании обобщенного закона Ома можем написать для каждой из сторон:

,

,

.

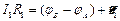Сложив эти уравнения, получим второй закон Кирхгофа:

.

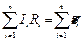Второй закон Кирх­гофа: в любом замкнутом контуре электрической цепи алгебраи­ческая сумма падений напряжений на участках цепи замкнутого контура равна алгеб­раической сумме ЭДС, включенных в этот контур.

Произведение IR называют падением напряжения на со­противлении R. Величинам IR и величинам E приписывают знаки. Если направление обхода контура, выбранное произвольно, на­пример по часовой стрелке, совпадает с направлениями тока и ЭДС они имеют знак + IR и + E. Если ток или ЭДС направлены против обхода, то они имеют знак -IR и - E.

Законы Кирхгофа позволяют выполнить расчет сложной электрической цепи, когда заданы схема цепи и значения всех R и E,а нужно вычислить силы токов I во всех участках цепи. На ос­новании первого и второго законов Кирхгофа составляют систе­му линейных уравнений, в которых неизвестными будут силы то­ков. Уравнений нужно составить столько, сколько в цепи иско­мых сил токов, причем эти уравнения должны быть математиче­ски линейно независимыми. Составленную систему уравнений решают обычно с помощью определителей или матриц. Найден­ное решение обязательно проверяют подстановкой.

Пример: дана схема цепи (рис. 2), в которой E ₁ = 6 В, E ₂ = 8В, r ₁ = 1 Ом, r ₂ = 2 Ом, R ₃ = 4 Ом. Указываются направления каждой ЭДС, от плюсового полюса источника во внешнюю цепь. Направления токов выбираются произвольно. Направление обходя контура выбирается произвольно. На рис. 2 все направления токов указаны в одну сторону.

По первому закону Кирхгофа для узла В: . По второму закону Кирхгофа для контура ABFKA: , а для контура АСДКА: . Подставляя исходные числовые данные, получают систему ли­нейных уравнений. Поскольку необходимо определить три тока, потребуется только три независимых уравнения: одно на первый и два на второй законы Кирхгофа.

.

Расширенная матрица системы:

.

Решив эту систему, получают A, А, А. Знак минус у тока I ₃ означает, что действительное на­правление этого тока обратно указанному на схеме. Проверка ре­шения: 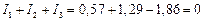.