|
Если диполь поместить в однородное электрическое поле, то полная действующая на него сила будет равна нулю. Действующие на заряды диполя силы равны по модулю и противоположны по направлению
Эти силы приложены в разных точках, образуя, так называемую пару сил. Пара сил создает вращающий момент. Модуль момента пары сил равен произведению силы на плечо, т. е. 
, где h — есть плечо пары сил (кратчайшее расстояние между линиями действия сил). Учитывая, что сила, действующая на заряд со стороны поля равна 
, а плечо пары сил 
(см. рисунок, 
— угол между векторами 
и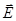 
), запишем 
. Произведение 
равно дипольному моменту 
, тогда
.
.Вектора 
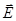, и 
образуют правовинтовую систему, что позволяет нам записать выражение для вращающего момента в векторном виде:
.
При двух ориентациях диполя — по полю (
) и против поля (
) момент сил обращается в нуль. Первая ориентация () соответствует устойчивому равновесию, вторая () — неустойчивому. Момент сил стремится повернуть диполь так, чтобы его электрический момент установился по направлению внешнего поля .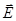
|
В неоднородном электрическом поле на диполь кроме ориентирующего момента сил будет действовать результирующая сила, втягивающая диполь в область с большей напряженностью. Пусть 
и 
— напряженности внешнего поля в точках, где расположены положительный и отрицательный заряды диполя. Тогда результирующая сила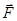 
, действующая на диполь равна (см. рисунок)
, (1)
где 
— сила, действующая на заряд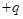 
диполя, 
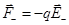— сила, действующая на отрицательный заряд 
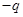диполя. Разность 
— это приращение вектора 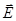на отрезке, равном длине диполя 
в направлении вектора 
. Вследствие малости этого отрезка можно записать
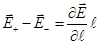, (2)
где 
— есть производная вектора 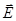по направлению , характеризующая изменение вектора 
на единицу длины в этом направлении. После подстановки (2) в (1) и учитывая, что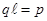 
получим,
.
