Рассматривая грани поляризационной пластины как бесконечно заряженные плоскости, запишем: 
. Тогда равенство (8) принимает вид: 
. Так как 
, то 
. Отсюда 
. Величину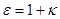 
назвали относительной диэлектрической проницаемостью среды. Относительная диэлектрическая проницаемость среды 
показывает во сколько раз напряженность поля в диэлектрической среде, в результате ее поляризации, меньше чем поле, которое было бы в отсутствии диэлектрической среды.
Введем еще одно соотношение, связывающее сторонние заряды на металлической пластине конденсатор а и поляризационные заряды на поверхности диэлектрика. Формулу (6) с учетом того, что 
, 
, запишем в виде 
. После преобразований 
, 
найдем искомое соотношение
.
Вектор электрической индукции (электрического смещения)
Поскольку источниками поля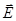 
являются все электрические заряды — сторонние и связанные, теорему Гаусса для поля 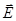можно записать так:
, (9)
где 
и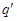 
сторонние и связанные заряды, охватываемые поверхностью S. Появление связанных зарядов усложняет дело и теорема Гаусса в этом виде оказывается малополезной для нахождения поля 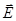. Это затруднение, однако, можно обойти, если выразить заряд 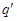через поток вектора 
по формуле (6). Тогда теорему Гаусса можно преобразовать к такому виду: 
. Перенесем интеграл с правой части в левую часть:
Величину, стоящую под интегралом в скобках обозначают буквой 
, и называют вектором электрической индукции (электрического смещения). Итак, мы нашли вспомогательный вектор, :
, (10)
поток которого сквозь произвольную замкнутую поверхность равен алгебраической сумме сторонних зарядов, охватываемых этой поверхностью:
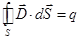. (11)
Это утверждение называют теоремой Гаусса для поля вектора . Заметим, что вектор представляет собой сумму совершенно различных величин: 
и . Поэтому он вспомогательный вектор, не имеющий какого-либо глубокого физического смысла. Размерность вектора та же, что вектора . Единицей величины служит кулон на квадратный метр (
).
