|
С помощью теоремы Гаусса рассчитаем электростатическое поле, создаваемое бесконечной заряженной плоскостью с плотностью + s, постоянной во всех точках плоскости. По соображениям симметрии можно считать, что силовые линии перпендикулярны плоскости, направлены от неё в обе стороны и имеют всюду одинаковую густоту. То есть поле бесконечной равномерно заряженной плоскости является однородным. для В качестве замкнутой поверхности применения теоремы Гаусса выберем поверхность цилиндра, построенного следующим образом: образующая цилиндра параллельна силовым линиям, а основания имеют площади S параллельны заряженной плоскости и лежат по разные стороны от нее. Поток напряженности поля через боковую поверхность равен нулю, поэтому полный поток через замкнутую поверхность равен сумме потоков через основания цилиндра: 
. По теореме Гаусса этот же поток определяется зарядом той части плоскости, которая лежит внутри цилиндра, и равен 
. Сравнивая эти выражения для потока 
, находим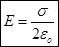 
.
Для равномерно заряженной пластины конечных размеров полученное выражение приближенно справедливо в области, находящейся достаточно далеко от краев пластины и не слишком далеко от ее поверхности.
