При перемещении в поле от исследуемой точки значение потенциала изменяется.
Вектор градиента потенциала электрического поля направлен в сторону увеличения потенциала перпендикулярно к эквипотенциальной поверхности. Отношение бесконечно малого изменения потенциала к бесконечно малому перемещению в этом направлении принимает максимальное значение, а по модулю вектор градиента равен этому отношению.
Математически это можно записать в виде
,
где 
— единичный вектор, направленный в сторону увеличения потенциала перпендикулярно к эквипотенциальной поверхности. Единица измерения градиента — В/м.
|
На рис. показаны две эквипотенциальные поверхности, соответствующие потенциалам 
и 
. Из рисунка видно что, 
, т.к. 
.
Работа сил поля по переносу заряда из точки 1 в точку 2 вдоль нормали равна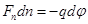 
, учитывая что 
, получим 
. Сократив на величину заряда 
и разделив обе части равенства на величину перемещения 
, получим связь между напряженностью и градиентом потенциала
.
Из этого соотношения видно, что вектор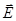 
направлен по нормали к эквипотенциальной поверхности в сторону убывания потенциала, т. е. вектора напряженности поля и градиента потенциала равны по модулю, но противоположны по направлению: 
.
Градиент и напряженность измеряются в одних и тех же единицах — В/м.
Вектор градиента 
в декартовых прямоугольных координатах имеет вид: 
, где частные производные 
потенциала j по x, y, и z являются проекциями вектора градиента соответственно на оси x, y, z. Используя, векторно-дифференциальный оператор «набла» — 
, запишем градиент как произведение этого оператора на потенциал j, 
, тогда вектор напряженности электрического поля записывают в виде 
.
