Стержень консольного типа нагружен двумя силами: величиной F в вертикальной плоскости и величиной 2F в горизонтальной плоскости. Параметр длины 
. Изготовлен стержень из Ст3 с допускаемым напряжением [σ]=160 МПа.
Требуется:
1. Определить грузоподъемность стержня [ F ] из условия прочности по допускаемому напряжению для прямоугольного сечения с соотношением сторон 
и величиной 
;
2. Определить грузоподъемность стержня [ F ] из условия прочности по допускаемому напряжению для круглого сечения, равного по площади прямоугольному профилю.
Решение
1. Определим положение опасного сечения, для чего построим эпюры изгибающих моментов МY и МХ на одной базе:
Из эпюр видно, что опасное сечение находится в заделке с моментами МХ = 3Fl и МY = 2Fl.
2. Определим положение силовой линии в плоскости прямоугольного и круглого сечений. Для этого с сохранением масштаба перенесем ординаты изгибающих моментов с эпюр МX и МY в опасном сечении в плоскость прямоугольного и круглого сечений и определим величину и направление ординаты суммарного момента 
, как геометрическую сумму моментов МX и МY.
3. Определим положение опасных точек в опасном сечении. В прямоугольном сечении опасными будут угловые точки «В» и «С» в силовых четвертях, а в круглом сечении точки «К» и «L» на концах диаметра, совпадающего с силовой линией.
4. Запишем условие прочности для опасных точек прямоугольного профиля и определим из его решения величину грузоподъемности [ F ]:
.
Предварительно выразим моменты сопротивления через характерный размер b поперечного сечения:
; 
.
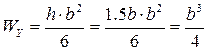После подстановки численного значения изгибающих моментов в сечении заделки и выражений для моментов сопротивления через размер b получим:
, откуда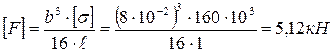 
.
5. Для круглого сечения определим из условия равенства площадей прямоугольного и круглого сечений величину диаметра:
.
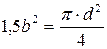
6. Для опасных точек круглого сечения «К» и «L» запишем условие прочности:
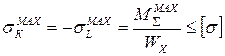, где 
.
Подставив в условие прочности, получим:
, откуда
.
Задача решена. 
2.3. 
Потренируемся?
· Пройти тестовый тренинг (Приложение 1, тесты к теме 2, стр. 96)
