Что такое косой изгиб?
Косым изгибом называется такой вид деформации, при котором силовая линия не совпадает ни с одной из главных центральных осей сечения.
Что такое силовая линия?
Силовая линия – это след плоскости действия изгибающего момента.
Что такое главные центральные оси сечения?
Это оси, проходящие через центр тяжести поперечного сечения, относительно которых центробежный момент инерции равен 0. Что-то опять сложно и не понятно! Ведь надо знать, что такое центробежный момент инерции 
! В простых случаях поперечных сечений, если хотя бы одна из осей координат сечения является осью симметрии, а вторая проходит через центр тяжести, такая система координат всегда главная.
Почему необходимо знать об этом виде деформации и уметь делать расчеты на прочность?
Дело в том, что косой изгиб достаточно часто встречается в реальных конструкциях и опаснее прямого. Поэтому, если условия работы элемента конструкции приводят к возникновению именно косого изгиба, то абсолютно очевидно, что надо уметь корректно оценивать прочность, учитывая особенности данного вида деформации.
Чтобы научиться оценивать прочность в случае косого изгиба надо знать! 
1. Косой изгиб можно представить как сумму двух прямых изгибов:
2. Напряжения при косом изгибе в любой произвольной точке поперечного сечения определяются как алгебраическая сумма нормальных напряжений от каждого изгибающего момента, создающего прямой изгиб:
,
Здесь х и у – координаты точки сечения, в которой определяют величину напряжения 
; 
и 
– главные осевые моменты инерции поперечного сечения. Для заданной формы сечения формулы для них можно найти в справочнике.
3. Для определения положения опасных точек сечения надо знать положение нейтральной линии, которая не перпендикулярна силовой (в отличие от прямого изгиба) и проходит через четверти, противоположные тем, через которые проходит силовая линия. Точки сечения, наиболее удаленные от нейтральной линии – опасные точки. Для прямоугольного сечения и форм сечений на основе прямоугольника (двутавр, швеллер) – это всегда угловые точки, находящиеся в силовых четвертях. Т.е. в четвертях, через которые проходит силовая линия.
4. Определить положение опасных точек можно также, используя прием простановки знаков нормальных напряжений в четвертях сечения от каждого из прямых изгибов относительно осей х и у, из которых состоит косой изгиб. Опасные точки находятся в четвертях сечения с одинаковыми знаками напряжений и максимально удалены от нейтральной линии и главных центральных осей сечения.
5. Условие прочности для косого изгиба:
.
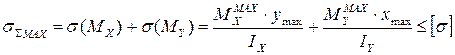6. Для элементов конструкций с симметричными формами профилей, изготовленных из пластичных материалов, можно использовать «зеркальную» формулу:
.
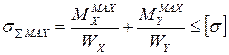Алгоритм расчета на прочность при косом изгибе 
1. Определение положения опасного сечения на элементе конструкции по эпюрам внутренних моментов 
и Му, построенных от действия внешних нагрузок.
2. Определение положения силовой линии в опасном сечении. Для этого необходимо в плоскости сечения по осям х и у отложить в масштабе ординаты внутренних моментов (Мх по оси у, а Му по оси х) в сторону, соответствующую положению ординат на эпюрах изгибающих моментов в опасном сечении. Ордината суммарного момента, построенная как геометрическая сумма ординат моментов Мх и Мy, 
определяет положение силовой линии.
3. Определение положения опасных точек в опасном сечении. Для сечения прямоугольной формы и подобной ему (двутавр, швеллер), опасные точки – это угловые точки в силовых четвертях. Они равноопасны, т.к. находятся на одинаковых расстояниях от главных центральных осей сечения.
4. Запись условия прочности для опасных точек и его решение согласно поставленной задаче:
.
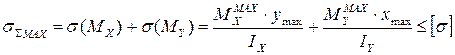Для прямоугольного сечения можно воспользоваться «зеркальной» формулой для определения нормальных напряжений от каждого изгибающего момента, создающего прямой изгиб:
,
где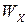 
и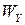 
– моменты сопротивления поперечного сечения относительно соответствующих главных центральных осей.
