Консольный стержень прямоугольного сечения на свободном конце нагружен сосредоточенной силой F =10 кН, вектор которой проходит через центр тяжести сечения под углом 30˚ к вертикальной оси y. Длина стержня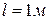 
, а соотношение сторон прямоугольного сечения 
. Стержень изготовлен из Ст3 с допускаемым напряжением [σ]=160 МПа.
Требуется:
1. Определить из условия прочности по допускаемым напряжениям величину характерного размера прямоугольного сечения [ b ].
2. Заменив прямоугольное сечение стержня круглым, определить величину диаметра круглого сечения [ d ] из условия прочности.
3. Сравнить металлозатраты стержней прямоугольного и круглого поперечных сечений.
Решение
1. Определим положение опасного сечения. Для этого спроектируем силу F на главные центральные оси Х и Y поперечного сечения: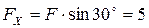 
кН; 
кН. Затем от каждой из этих сил построим эпюры изгибающих моментов на одной базе МY и МХ,соответственно. Опасное сечение будет в заделке, т.е. в том сечении, где моменты достигают своего максимального значения.
2. Определим положение силовой линии в опасном сечении. Для этого изобразим сечение, в плоскости которого отложим в масштабе значения изгибающих моментов МY и МX в ту же сторону, что на эпюрах соответствующих моментов: МY отложим вправо, а МX отложим вверх. Т.к. эпюры построены на растянутых волокнах, то растянуты правые волокна стержня относительно оси «у» от действия момента МY и, соответственно, там поставим знаки «+» в I и IV четвертях сечения, а в противоположных II и III знаки «–» (нумерацию четвертей прямоугольника смотри ниже). Также растянуты верхние волокна стержня относительно оси «х» от момента МX и, соответственно, поставим знаки «–» нормального напряжения в I и II четвертях, а в нижних (Ш и IV) четвертях знаки «+». Тогда ордината суммарного момента пройдет через I и III четверти и определит положение силовой линии. В этих же четвертях совпадают знаки нормальных напряжений от изгибающих моментов МX и МY:
3. Определим положение опасных точек в опасном сечении. Это будут угловые точки в силовых четвертях, т.е. точки «В» и «С». Точки являются равноопасными точками, т.к. величины напряжений в них будут одинаковыми по абсолютной величине. В точке «С» – угловой точке третьей четверти с двумя знаками «–» нормальных напряжений от двух прямых изгибов возникает максимальное сжимающее напряжение. Противоположная ей точка «В» попала в область растяжения (два знака «+» от прямых изгибов) и напряжение в ней будет положительным: 
.
4. Запишем условие прочности для опасных точек и определим из его решения величину размера поперечного сечения:
.
Предварительно выразим моменты сопротивления поперечного сечения через характерный размер b.
; 
.
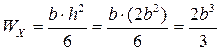После подстановки численного значения изгибающих моментов в сечении заделки и выражений для моментов сопротивления через размер b получим:
, откуда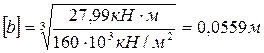 
.
5. Для определения диаметра круглого сечения для данного стержня определим внутренний изгибающий момент в заделке: 
. В плоскости опасного сечения проведем ординату максимального момента под углом в 30˚ к оси y и продлим ее до пересечения с контуром сечения. Это и будет силовой линией. Нейтральная линия проходит перпендикулярно силовой линии. Опасными точками будут точки, расположенные на максимальном расстоянии от нейтральной линии. Это точки «К» и «L», находящиеся на концах диаметра, совпадающего с силовой линией. Направление вектора внешней силы F указывает на сжатую зону. Т.е. половина сечения выше нейтральной линии растянута и точка «К» испытывает положительные напряжения. Соответственно, точка «L» – отрицательные напряжения.
6. Запишем условие прочности по формуле прямого изгиба:
.
Для круглого сечения момент сопротивления через диаметр определяется как:
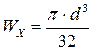
Подставив в условие прочности значение момента и выражение для WX, получим:
, откуда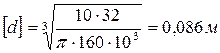 
.
7. Сравним стержни прямоугольного и круглого сечений по металлозатратам. Для этого определим площади сечений:
,
т.е. для случая косого изгиба (прямоугольный профиль) требуется большее по площади сечение, что указывает на более опасный характер этого вида деформации для данных исходных условий.
Задача решена. 
