Задача
Статически неопределимая балка постоянного поперечного сечения нагружена заданной системой поперечных сил и изгибающих моментов.
Материал балки – Ст.3 с допускаемым напряжением 
=160МПа и модулем Юнга Е= 
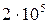МПа.
Требуется:
Раскрыть статическую неопределимость балки, подобрать из условия прочности размер двутаврового сечения и проверить выполнение условия жесткости, приняв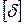 
=0,8 мм.
Решение
1. Определим степень статической неопределимости балки s.
Для этого сначала найдем суммарное количество реактивных усилий в опорах балки. В жесткой заделке Е их 2 (реактивный момент и вертикальная реактивная сила), в подвижных шарнирных опорах D и В – по одной вертикальной реактивной силе (см. Практикум, часть 1, стр. 55-56). Итого – 4 реактивных усилия.
Затем определим необходимое и достаточное количество уравнений статического равновесия. Для плоской балки с вертикальной нагрузкой количество уравнений равновесия равно двум (см. Практикум, часть 1, стр. 57-58).
Таким образом, степень статической неопределимости балки равна:
,
т.е. данная балка дважды статически неопределима.
2. Выберем основную систему. Для этого нужно убрать с балки всю действующую нагрузку и отбросить лишние связи, чтобы она стала статически определимой, оставаясь при этом кинематически неизменяемой (т.е. неподвижной). К статически определимым балкам относятся балки с жестким защемлением и балки на двух шарнирных опорах, одна из которых шарнирно-неподвижная, а другая – шарнирно-подвижная (см. Практикум, часть 1, стр. 56).
Рассмотрим возможные варианты основных систем.
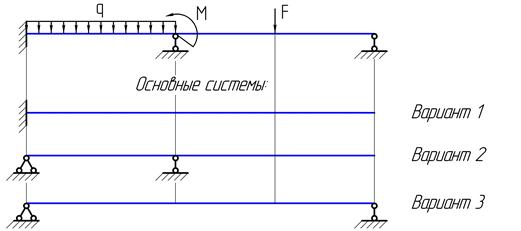
Любая из трех вариантов основных систем может быть использована для раскрытия статической неопределимости заданной балки. Которая же из трех является наиболее рациональной? 
Учитывая, что в процессе решения на основной системе неоднократно придется строить различные эпюры, то можно считать, что основная система с жесткой заделкой (вариант 1) является наиболее рациональной (применяя метод сечений в направлении от свободного конца к заделке, нет необходимости определять в ней реактивные усилия). Рекомендация: если в исходной статически неопределимой системе есть хотя бы одна жесткая заделка, то при образовании основной системы эту заделку нужно оставить, а остальные опоры отбросить.
Внимание! 
Если в исходной статически неопределимой балке нет ни одной жесткой заделки, а только шарнирные опоры, то в качестве основной системы может служить только балка на двух шарнирных опорах, одна из которых шарнирно-неподвижная, а другая – шарнирно-подвижная.
Итак, для дальнейшего решения выбираем первый вариант основной системы:
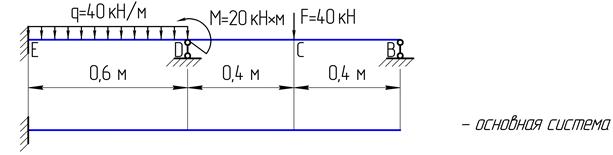
3. Образуем эквивалентную систему из выбранной основной. Для этого на основной системе показываем заданную внешнюю нагрузку и реакции отброшенных шарнирно-подвижных опор, обозначая их Х1 и Х2:
Направления для Х1 и Х2 выбираем произвольно (вверх или вниз), а решение нам покажет, верны они или нет.
4. Запишем условие эквивалентности в виде системы канонических уравнений метода сил (СКУМС). Для дважды статически неопределимой системы оно имеет следующий вид:
5. Определим коэффициенты СКУМС.
5.1. Построим вспомогательные эпюры изгибающих моментов: грузовую и две единичных.
Построим грузовую эпюру изгибающих моментов МxF. Она строится на основной системе только от действия заданной внешней нагрузки:
Здесь значения моментов в граничных сечениях балки определяются методом сечений в направлении от свободного края к заделке. Эпюра строится на растянутых волокнах (см. Практикум, часть 1, стр. 11-19).
Участок ВС не нагружен, момент во всех сечениях равен нулю:
.
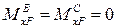На участке СD прямолинейная зависимость, т.к. участок без распределенной нагрузки.
.
В сечении D приложен сосредоточенный момент, вызывающий на эпюре скачок на величину момента М=20 
в сторону растянутых волокон (вниз).
На участке DE парабола, т.к. участок с распределенной нагрузкой. Выпуклость параболы вниз (в сторону действия распределенной нагрузки).
.
На грузовой эпюре также показаны значения момента в средних сечениях каждого ненулевого участка. Эти значения нам потребуются при «перемножении» эпюр по формуле Симпсона. Определяются они аналогично (предлагается получить эти значения самостоятельно).
Построим единичные эпюры изгибающих моментов 
и 
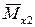. Единичные эпюры строятся на основной системе от действия каждой «лишней» неизвестной, принятой равной безразмерной единице: 
и 
.
Здесь значения единичных моментов в граничных и средних сечениях участков равны произведению единичной силы на соответствующее плечо (расстояние от точки приложения силы до соответствующего сечения).
5.2. Найдем единичные коэффициенты СКУМС.
Единичные коэффициенты 
определяются путем «перемножения» соответствующих единичных эпюр методом Мора (см. Практикум, часть 1, стр. 41). Интеграл Мора при этом будем вычислять по формуле Симпсона (см. там же, стр. 42, формула (2)).
Коэффициент 
находим «перемножением» первой единичной эпюры на , т.е. умножаем её саму на себя (индексы коэффициента показывают, какая эпюра на какую «перемножается»). Участков перемножения три: ВС, СD и DE.
.
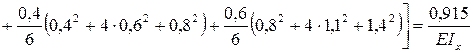Аналогично находим коэффициент 
«перемножением» первой единичной эпюры на вторую 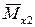. Участок перемножения один – DE, т.к. на участках ВС и СD эпюра 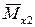нулевая.
.
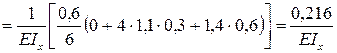Очевидно, что симметричные коэффициенты равны между собой:
.
Коэффициент 
находим путем «перемножения» второй единичной эпюры 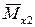на саму себя. Участок «перемножения» один: DE.
.
5.3. Найдем грузовые коэффициенты СКУМС.
Грузовые коэффициенты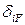 
находятся путем «перемножения» соответствующей единичной эпюры 
на грузовую 
. Найдем их методом Мора, также применяя формулу Симпсона.
.
.
6. Подставим найденные коэффициенты в СКУМС и решим полученную систему двух линейных алгебраических уравнений относительно «лишних» неизвестных Х1 и Х2.
Отметим, что в каждом слагаемом обоих уравнений в знаменателе стоит величина EIx – жесткость поперечного сечения балки. Следовательно, на эту величину оба уравнения можно сократить, тогда система принимает вид:
В результате математического решения этой системы находим значения «лишних» неизвестных: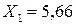 
кН, 
кН. Оба значения получились положительными, следовательно, мы угадали истинное направление этих усилий. Внимание! Если значение «лишней» неизвестной получается отрицательным, значит нужно изменить её направление на эквивалентной системе на противоположное.
7. Построим суммарную эпюру изгибающих моментов 
. Суммарная эпюра строится на основной системе с учетом действия заданной нагрузки и найденных значений «лишних» неизвестных.
Определим значения моментов в граничных сечениях суммарной эпюры:
, 
,
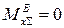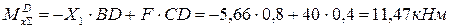(до скачка),
(после него),
.
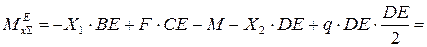
На суммарной эпюре показаны также значения моментов в средних сечениях участков. Они находятся аналогично методом сечений (предлагается получить эти значения самостоятельно).
8. Сделаем деформационную проверку. Убедимся, что вертикальные перемещения раскрепленных точек эквивалентной системы 
и 
равны нулю. Для нахождения этих перемещений методом Мора необходимо каждую единичную эпюру и 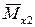«перемножить» на суммарную . Учитывая, что значения Х1 и Х2 были найдены неточно (с учетом округления), точного нуля в деформационной проверке мы не получим. Допустимая погрешность решения – не более 3%.
Для сечения В:
.
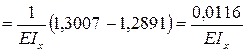Для определения точности решения необходимо сгруппировать значения с разными знаками (что сделано в последней строке) и оценить погрешность вычислений в процентах по отношению к положительной составляющей:
% 
% 
% =0,9%,
что допустимо.
Для сечения D:
.
% = 
% = 
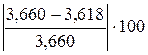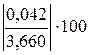% =1,1%,
что тоже допустимо.
Таким образом, статическая неопределимость балки раскрыта верно.
9. Подберем из условия прочности размер двутаврового сечения балки (см. Практикум, часть 1, стр. 37). Определим по суммарной эпюре положение опасного сечения. Сечение D наиболее опасно, т.к. в этом сечении наибольший изгибающий момент:
.
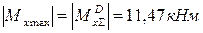Заданная балка изготовлена из пластичного материала, следовательно, условие прочности имеет вид (см. Практикум, часть 1, стр. 35):
.
Найдем из условия прочности допускаемую величину момента сопротивления:
.
Таким образом, двутавровое сечение балки должно иметь величину момента сопротивления, не меньшую, чем 71,7 см3. По сортаменту прокатной стали (ГОСТ 8239-89) подберем подходящий номер двутавра (см. Приложение 4, таблица 4.1, стр. 152). Подходит двутавр №14, у которого осевой момент сопротивления Wx =81,7см3, а осевой момент инерции Ix =572 см4.
10. Определим перемещения (прогибы) некоторых незакрепленных сечений балки, изобразим приближенный вид её изогнутой оси и проверим выполнение условия жесткости (см. Практикум, часть 1, стр. 40).
При расчете на жесткость балки используем поперечное сечение, которое подобрали из условия прочности – двутавр № 14 с осевым моментом инерции 
.
Перемещения обычно определяют в двух-трех незакрепленных граничных сечениях балки, однако, в заданной балке такое граничное сечение единственное – С. Тогда в качестве второго сечения можно взять середину самого длинного участка. Мы возьмем сечение К – середину участка ЕD.
Определим методом Мора перемещения в сечениях С и К. Для этого построим две единичных эпюры М1С и М1К, приложив поочередно в каждом сечении по единичной силе. Внимание! Единичные эпюры здесь строятся на выбранной основной системе.
Перемещение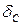 
найдем путем «перемножения» единичной эпюры М1С на суммарную эпюру :
.
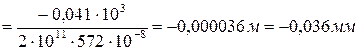Знак «–» здесь говорит о том, что истинное перемещение сечения С противоположно выбранному направлению единичной силы на эпюре М1С. Следовательно, сечение С балки перемещается вверх на 0,036мм.
Перемещение 
найдем путем «перемножения» единичной эпюры М1К на суммарную эпюру :
.
Направление перемещения сечения К совпадает с выбранным направлением единичной силы на эпюре М1С. Следовательно, сечение К балки смещается вниз на 0,11мм.
Изобразим приближенный вид изогнутой оси балки, учитывая следующие условия:
· Закрепленные сечения В, D и Е балки не смещаются (остаются на месте).
· Сечение С смещается вверх на 0,036мм, а сечение К вниз на 0,11мм.
· Изогнутая ось балки от жесткой заделки Е отходит с нулевым углом поворота.
· Направление выпуклости изогнутой оси определяется по суммарной эпюре . Учитывая, что эпюра моментов строится на растянутых волокнах, получаем, что на участках, где суммарная эпюра расположена выше оси, выпуклость изогнутой оси балки направлена вверх. Соответственно, там, где расположена ниже оси, балка изгибается выпуклостью вниз.
Учитывая все вышеизложенное, изображаем приближенный вид изогнутой оси балки.
Очевидно, что максимальный прогиб балки, если и отличается от прогиба в сечении К, то весьма несущественно. Принимаем 
.
Проверим выполнение условия жесткости:
– условие жесткости выполняется.
Задача решена. 