1. С какой наибольшей скоростью может возрастать функция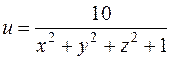 
при переходе точки 
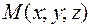через точку 
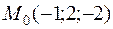? В каком направлении должна двигаться точка М при переходе через точку 
, чтобы функция убывала с наибольшей скоростью?
Наибольшая, по абсолютной величине, скорость изменения функции при переходе точки М через точку Р численно равна модулю градиента функции в точке Р. При этом функция будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точка М при переходе через точку Р двигаться по направлению градиента функции в точке Р или по прямо противоположному направлению. Руководствуясь этими положениями, находим частные производные функции и ее градиент в любой точке:
(2)
Далее находим градиент в указанных точках, подставив их координаты в выражение (2):
1) 
,
его модуль, численно равный искомой наибольшей скорости возрастания данной функции при переходе М через точку М0, равен:
.
2) 
,
Искомый вектор, имеющий прямо противоположное направление, будет
.
Чтобы функция убывала с наибольшей скоростью, при переходе через точку М1 точка М должна двигаться в направлении вектора 
.
[1] Предполагается, что функция — однозначная непрерывная функция, имеющая непрерывные частные производные первого порядка,,.
