1. Вычислить производную функции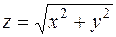 
в точке 
по направлению:
а) биссектрисы первой координатной четверти.
б) радиуса-вектора точки А.
в) вектора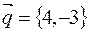 
.
1) Находим частные производные функции и вычисляем их значения в точке А:
, 
, 
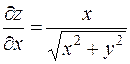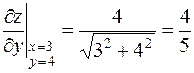
Подставляя в формулу (1), найдем производные функции 
в точке А по любому направлению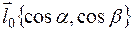 
.
2) найдем значения производной по указанным направлениям:
а) Для биссектрисы первого координатного угла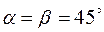 
, откуда искомая производная равна
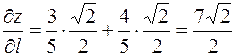
б) запишем координаты радиуса-вектора точки А: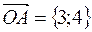 
, и найдем направляющие косинусы: 
, 
.
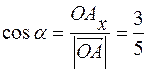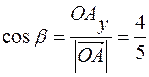Тогда для этого случая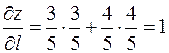 
.
в) направляющие косинусы вектора :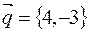 
, 
.,
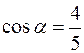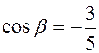откуда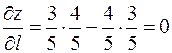 
.
2. Вычислить производную функции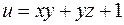 
по направлению вектора 
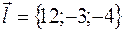в любой точке и в точках 
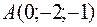и 
.
1) Находим частные производные функции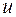 
:
, 
, 
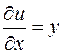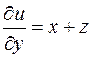и направляющие косинусы вектора 
, модуль которого 
:
, 
, 
.
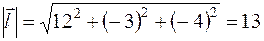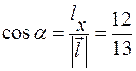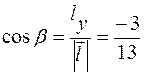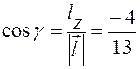2) Подставляя в (1), найдем производную функции 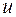по указанному направлению 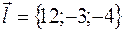в любой точке:
.
3) Подставляя координаты точек А и В, получим производные функции
, 
.
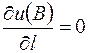3. Найти производную функции 
в точке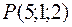 
в направлении, идущем от этой точки к точке 
.
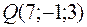1) Находим частные производные функции и вычисляем их значения в точке Р:
, 
, 
, 
, 
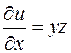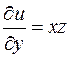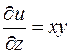
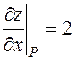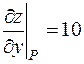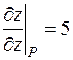
2) найдем координаты вектора: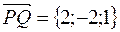 
, его модуль 
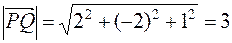и вычислим его направляющие косинусы: 
, 
, 
.
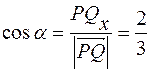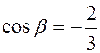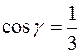Отсюда 
.
Знак минус указывает, что в данном направлении функция убывает.
4. Найти точки, в которых функция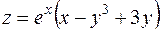 
стационарна (т.е. точки, в которых производная по любому направлению равна нулю).
Для того чтобы в некоторой точке функция была стационарна, необходимо и достаточно, согласно формуле (1), чтобы в этой точке все ее частные производные первого порядка одновременно обращались в нуль.
Найдем частные производные первого порядка:
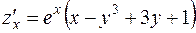и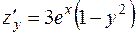 
.
Решив систему уравнени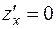й: 
и 
, получим 2 точки, в которых функция стационарна: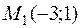 
. и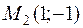 
.
3. Градиент функции
Снова рассмотрим формулу производной по направлению:
.
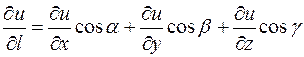Вторые множители в каждом из этих слагаемых являются, как мы уже отмечали, проекциями единичного вектора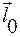 
, направленного по вектору : 
.
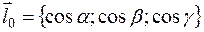Возьмем теперь вектор, проекциями которого на координатные оси будут служить значения частных производных в выбранной точке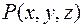 
. Назовем его градиентом функции 
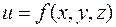и будем обозначать символами:
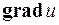или 
.
1°. Пусть 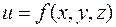— однозначная непрерывная функция, имеющая непрерывные частные производные Градиентом скалярной функции 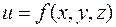называется вектор, проекции которого на координатные оси Ох, Оу и Oz соответственно равны значениям частных производных этой функции 
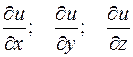, т. е.
.
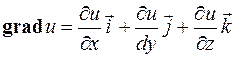На основании этого определения проекции вектора 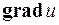на координатные оси запишутся так:
; 
; 
.
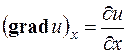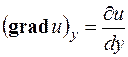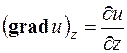Модуль вектора 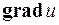вычисляется по формуле:
.
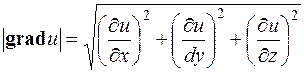Подчеркнем, что проекции градиента зависят от выбора точки 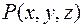и изменяются с изменением координат этой точки. Таким образом, каждой точке скалярного поля, задаваемого функцией поля 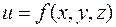, соответствует определенный вектор – градиент этой функции.
Связь градиента с производной по направлению
Из определения градиента следует, что производная функции по данному направлению равна скалярному произведению градиента функции на единичный вектор этого направления:
.
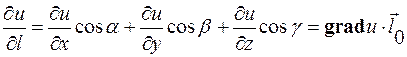Из определения скалярного произведения:
,
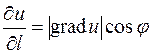где j - угол между 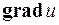и . Отсюда видно, что производная по направлению достигает наибольшего значения, когда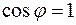 
, т.е. при j=0. Причем это наибольшее значение 
.
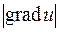Итак, направление градиента есть направление наискорейшего возрастания функции.
