Построить линии уровня функций, соответствующие значениям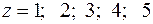 
.
а) 
.
Полагая 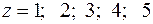, получим уравнения соответствующих линий уровня:
, 
, 
, 
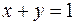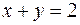и 
.
Построив эти линии в декартовой системе координат хОу, получим прямые, параллельные биссектрисе второго и четвертого координатных углов (рис.1)
б) 
.
Напишем уравнения линий уровня:
, 
, 
, 
и 
.
Построив их в плоскости хОу, получим концентрические окружности с центром в начале координат (рис.2)
в) 
.
Линии уровня этой функции 
, 
, 
, 
и 
представляют собой параболы, симметричные относительно Оу с общей вершиной в начале координат (рис. 3).
2. Производная по направлению
Важной характеристикой скалярного поля является скорость изменения поля в данном направлении.
Для характеристики скорости изменения поля 
в направлении вектора 
вводят понятие производной поля по направлению.
Рассмотрим функцию 
в точке 
и точке 
.
Проведем через точки 
и 
вектор . Углы наклона этого вектора к направлению координатных осей х, у, z обозначим соответственно a, b, g. Косинусы этих углов называются направляющими косинусами вектора .
Расстояние между точками и на векторе обозначим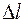 
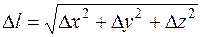
Высказанные выше предположения, проиллюстрируем на рисунке:
Далее предположим, что функция непрерывна и имеет непрерывные частные производные по переменным х, у и z. Тогда правомерно записать следующее выражение:
,
где величины e1, e2, e3 – бесконечно малые при 
.
Из геометрических соображений очевидно:
Таким образом, приведенные выше равенства могут быть представлены следующим образом:
;
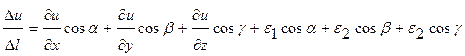Из этого уравнения следует следующее определение:
1°. Пусть задана точка и вектор 
, выходящий из точки (рис.). Производной функции по направлению вектора 
называют предел отношения разности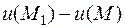 
к величине направленного отрезка 
, когда точка стремится к точке , оставаясь на прямой 
:
.
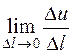Производная от функции по направлению обозначается:
или 
.
Эта производная вычисляется по формуле (при условии, что функция дифференцируема в точке М):
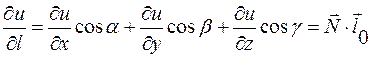, (1)
где 
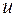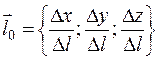- нормальный вектор к поверхности уровня функции 
,
или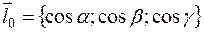 
- единичный вектор (т.е. его длина равна единице), характеризующий направление вектора .
- направляющие косинусывектора .
Заметим, что
1) величина 
является скалярной. Она лишь определяет направление вектора .
2) В каждой точке, где функция дифференцируема, она имеет бесконечное множество производных по различным направлениям.
