1) Из всех производных функции, взятых по различным направлениям, наибольшее значение всегда имеет производная по направлению градиента функции. Поэтому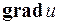 
есть вектор скорости наибыстрейшего возрастания функции. При этом 
равен числовому значению наибольшей скорости изменения скалярного поля.
2) Скалярное поле убывает быстрее всего в направлении, противоположном вектору 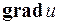, со скоростью, равной .
3) Вектор 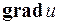в каждой точке направлен по нормали к поверхности (или линии) уровня поля, проходящей через эту точку, в сторону возрастания функции.
Скорость изменения скалярной функции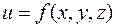 
по некоторому направлению 
равна проекции вектора 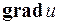на это направление , т. е.
.
В этом состоит основное свойство градиента функции.
Из последнего свойства вытекает, что производная по любому направлению, касательному к поверхности уровня, проходящей через данную точку, равна нулю.
Геометрическийсмысл градиента. С точки зрения геометрического представления градиент перпендикулярен поверхности уровня функции.
Физическийсмысл градиента. Градиент – вектор, показывающий направление наискорейшего изменения некоторого скалярного поля u в какой-либо точке (градиент температуры, градиент давления и т.п.).
При вычислениях применяют следующие свойства градиента:
.
