Случайные погрешности проявляются в том, что повторные измерения одной и той же величины, казалось бы в одних и тех же условиях, приводят к результатам, отличающимся один от другого. При исследовании случайных погрешностей используется аппарат математической статистики и теории вероятностей, решающих две группы задач:
1) проверка статистических гипотез
– о соответствии эмпирической функции распределения выбранной теоретической;
– о промахах;
2) обработка результатов наблюдений при различных видах измерений:
– при прямых однородных;
– косвенных;
– совместных;
– корреляционно связанных.
В настоящей работе ставится задача проверки перечисленных статистических гипотез при прямых равноточных измерениях.
Результаты наблюдения входного сопротивления исследуемой цепи, собранной из серийно изготовленных резисторов, могут быть получены двумя
путями:
выборочными измерениями входных сопротивлений электрических цепей, собранных из серийно изготовленных резисторов;
методом статистических испытаний (математическим моделированием действительных значений сопротивлений резисторов цепи в пределах допускаемых отклонений от номинальных с последующим вычислением входных сопротивлений).
В настоящей работе предлагается второй путь. При этом принимается во внимание, что распределение действительных значений сопротивлений резисторов в границах допускаемых отклонений изменяется по равномерному закону распределения. Разыгрывается по 60 моделей каждого из резисторов исследуемой цепи.
Для составления моделей можно использовать равнораспределенные случайные числа в интервале [0;1]. Так как интервалы, в которых моделируются характеристики, отличны от [0;1], то необходимо произвести некоторые преобразования над случайными числами.
Закон равномерного распределения (см. рис. 3.7) аналитически записывается в виде:
(3.77)
где b, a - границы допускаемого отклонения сопротивления резистора от номинального значения (максимальное и минимальное значения возможного разброса параметра).
Рис. 3.7. Плотность равномерного распределения
Функция распределения для равномерного закона на интервале [a, b]
(3.78)
где 
– значения сопротивления в интервале [a, b] с равномерным законом распределения.
Из выражения (3.78) можно вычислить xi:
(3.79)
где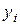 
– случайные числа в интервале [0; 1] (табл. 3.9).
Для определения модели входного сопротивления следует воспользоваться аналитическим выражением для расчета входного сопротивления исследуемой схемы замещения.
По полученным статистическим моделям параметров резисторов и входного сопротивления цепи строятся гистограммы. Шаг интервала гистограммы определяется в соответствии с формулой Стэджеса:
(3.80)
где 
и – максимальное и минимальное значения моделей каждого из параметров;
n – число моделей.
За начало каждого интервала рекомендуется принимать величину 
; начало второго интервала совпадает с концом первого: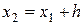 
; начало третьего – с концом второго: 
. Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет больше .
После установления шкалы интервалов следует сгруппировать результаты моделей. В интервал включаются данные, большие или равные нижней границе интервала и меньшие верхней границы. Вероятность попадания случайной величины в заданный интервал 
определяется выражением:
(3.81)
где 
– число моделей, попадающих в каждый интервал.
