Таблица2.17
Исследование резонанса
| Начальная фаза j, град | Модуль сопротивления Z, Ом | Частота генератора f, Гц |
| –60 | ||
| –30 | ||
2.6.4. Контрольные вопросы
1) Указать назначение электронного прибора ВМ507. Какие характеристики можно определить при помощи прямых измерений?
2) Провести анализ структурной схемы и временной диаграммы для измерения угла сдвига фаз (см. рис. 2.17 и 2.18).
3) Провести анализ измеренных значений и графика в опыте исследования резонанса напряжения при помощи прибора ВМ507.
4) Объяснить, почему для практических измерений выбирается частота, кратная 1,592. Объяснить, как пользоваться таблицей для прямых измерений
L и С (см. табл. 2.14 и 2.15).
3. ОБРАБОТКА РЕЗУЛЬТАТОВ НАБЛЮДЕНИЯ
3.1. Основные сведения из теории
Для ответа на вопросы "как обрабатывать измерительную информацию?", "что получили?" рассмотрим методы обработки результатов наблюдения с целью получения результата измерения.
Результат наблюдения (РН) – значение измеряемой величины, получаемое при отдельном наблюдении, или показание измерительного прибора.
Под результатом измерения (РИ) понимается совокупность трех
значений:
- измеряемой величины 
;
- погрешности 
;
- доверительной вероятности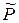 
, т. е. РИ = 
.
Определение значения измеряемой величины зависит от способов измерения. При однократном наблюдении в качестве результата измерения имеется одно число x 1, которое и принимается за значение измеряемой величины 
. При многократных равноточных наблюдениях значение измеряемой величины может быть найдено по формуле:
, (3.1)
где х i – результаты отдельных наблюдений;
n – количество наблюдений.
Величина содержит в себе как минимум три характеристики:
D c – систематическая погрешность;
u – неисключенные остатки систематической погрешности;
– случайная погрешность (в случае многократных наблюдений).
Задача по определению 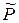связана с априорным назначением точности измерения.
3.1.1. Представление о погрешностях измерения
Любое измерение всегда ограничено по точности из-за несовершенства методов и средств измерения, влияния средств измерения на объект и т. д., поэтому всякий результат наблюдения является смещенным. Для оценки погрешности пользуются понятием абсолютной погрешности (D) – разности между реальной и номинальными характеристиками или значениями.
Абсолютная погрешность, взятая с обратным знаком, называется
поправкой:
. (3.2)
Сама по себе абсолютная погрешность не может служить показателем точности измерения, так как одно и тоже значение, например, D = 0,05 мм, при
х = 100 мм соответствует достаточно высокой точности, а при х = 1 мм – низкой, поэтому для характеристики результатов измерения вводят понятие относительной погрешности
, (3.3)
где х 0 - номинальное значение измеряемой величины.
Относительная погрешность выражается в относительных единицах или процентах. Для нормирования погрешности средств измерения используется приведенная погрешность
, (3.4)
где х к – предел измерения прибора.
Ее основное отличие от относительной погрешности состоит в том, что D относится не к текущей переменной величине х, а к постоянной величине –
номинальному значению.
3.1.2. Систематическая погрешность
Систематическая погрешность Dс характеризует степень близости полученного значения измеряемой величины к тому значению, которое может быть получено с максимально возможной точностью. Это проявляется в том, что всякий полученный результат наблюдения оказывается смещенным относительно точного результата.
Задача по исследованию и определению систематической погрешности является одной из самых сложных, поскольку не всегда ее можно обнаружить и исключить. В случае обнаружения систематической погрешности возможно ее вычисление и внесение поправки в результат наблюдения. Другой способ учета систематической погрешности – устранение ее схемотехнически или выбор другого метода измерения.
Рассмотрим пример исключения D с при проведении эксперимента, например, взвешивание на рычажных весах, т.е. определение массы тела m т. Одной из причин появления D с является разная длина плеч весов (l 1 » l 2). Если поместить m т на левую чашку весов (рис. 3.1), то можно записать:
m т l 1 g = m 1 l 2 g, (3.5)
где g – ускорение свободного падения;
m1 – масса гири.
Затем тело помещают на правую чашку весов (рис. 3.2) и уравновешивают гирей, которая имеет массу m 2. Массы m 1 и m 2 не равны из-за разности длин плеч весов и, следовательно, наличия D с. Итогом второго взвешивания становится следующее уравнение:
m 2 l 1 g = m т l 2 g. (3.6)
 | |||
 | |||
Рис. 3.1. Исходное измерение Рис. 3.2. Измерение с противопоставлением для устранения систематической для устранения систематической
погрешности погрешности
Взяв отношение выражений (3.5) и (3.6), получим:
, (3.7)
откуда
. (3.8)
В формуле (3.8) отсутствуют длины плеч весов, которые создают систематическую погрешность.
3.1.3. Оценка результирующей систематической погрешности и
внесение поправок
После анализа схемы измерения и вычисления систематических погрешностей имеется ряд значений Dсj, j = 1¸k. Каждая из Dс j имеет свою природу возникновения, а также свои значение и знак. Результирующая систематическая погрешность вычисляется по формуле:
, (3.9)
где k – количество вычисленных неисключенных погрешностей.
Затем вычисляют поправку
. (3.10)
Если 
, т. е. не зависит от времени, то ее можно внести в
среднее значение:
. (3.11)
В случае, когда 
является функцией времени, поправку вводят в каждый результат наблюдения:
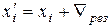, (3.12)
а затем определяют
. (3.13)
Внеся поправку в результат наблюдения, получают несмещенное значение измеряемой величины, которое является неокончательным, поскольку еще не учтены погрешности приборов и модельные составляющие погрешности измерения (погрешности сопротивления, емкости, индуктивности, температуры, источников питания и т. д.), т. е. все то, что относится к неисключенным остаткам систематической погрешности.
3.1.4. Неисключенные остатки систематической погрешности
Неисключенные остатки (НО) систематической погрешности (u) – это та ее часть, которая остается после оценки и устранения этой погрешности
(рис. 3.3).
 |
Рис. 3.3. Смещенный интервал неисключенных остатков
Исследование неисключенных остатков u предполагает выполнение следующей работы:
- анализ источников возникновения;
- оценка ui (i = 1, 2,..., k) по каждому источнику возникновения;
- оценка результирующей составляющей неисключенных остатков систематической погрешности.
Особенность исследования неисключенных остатков, представляющих собой составляющую систематической погрешности, заключается в том, что значения ui недетерминированы, т. е. представляют собой случайную величину, которую можно охарактеризовать средним квадратическим отклонением (СКО).
Тогда u рез соответствует свое результирующее СКО 
:
, (3.14)
где b i – функция влияния ui на конечный результат.
Если влияние компонентов на конечный результат неизвестно, то вводится гипотеза об одинаковом влиянии каждого компонента (bi = 1).
В том случае, когда закон изменения каждого компонента неизвестен и нет возможности определить хотя бы его вид, вводится гипотеза о том, что отдельные компоненты неисключенных остатков распределены равномерно. Реализация этой гипотезы позволяет для каждого u i выбрать границы Q i,
для u рез – Q рез:
, (3.15)
где k – поправочный коэффициент, зависящий от числа компонентов и доверительной вероятности.
Зависимость k от числа компонентов слабая. Значение коэффициента k при доверительной вероятности Р приведены в табл. 3.1.
Таблица 3.1
Значения коэффициента k в зависимости от числа слагаемых и
доверительной вероятности P
| Число слагаемых n | Значение погрешности k при доверительной вероятности Р | |||
| 0,9 | 0,95 | 0,99 | 0,9973 | |
| 0,97 | 1,10 | 1,27 | 1,34 | |
| 0,96 | 1,12 | 1,37 | 1,50 | |
| 0,96 | 1,12 | 1,41 | 1,58 | |
| 0,96 | 1,12 | 1,42 | 1,61 | |
| 0,96 | 1,12 | 1,42 | 1,64 | |
| … | … | … | … | … |
| ¥ | 0,95 | 1,13 | 1,49 | 1,73 |
Результат измерения при доверительной вероятности Р записывается в следующем виде:
. (3.16)
3.1.5. Пример обработки результата наблюдения
при однократном измерении
Производится измерение напряжения на сопротивлении. Известно:
R = (50 ± 1) Ом, вольтметр с внутренним сопротивлением Rv = 5 кОм, с относительной погрешностью внутреннего сопротивления di = 0,5 %. Верхний предел вольтметра V верх = 15 В, класс точности d = 1 %, шкала равномерная, число делений 150. Вольтметр показал значение Uv = 12,3 В. Необходимо
записать результат измерения.
Вариант 1
Погрешность 
может быть найдена из формулы класса точности
прибора
%; (3.17)
В.
Выбирая Р = 0,95, можно записать результат измерения:
В при Р = 0,95.
Результат смещен, поскольку не учитывалась методическая систематическая погрешность, обусловленная шунтированием сопротивления R сопротивлением вольтметра R v.
Вариант 2
|
поправки. Предполагая, что ток через R остается неизменным до и после включения вольтметра, можно определить Dс:
, (3.18)
где U = IR – истинное значение
Рис. 3.4. Измерение напряжения напряжения на R,
на резисторе и определение НО
. (3.19)
Подставив U и V в формулу для D с, получим:
. (3.20)
Значение I неизвестно, поэтому от абсолютных значений перейдем к относительным, т. е. вычислим относительную методическую погрешность
, (3.21)
относительная погрешность не зависит от показаний приборов, а также от значения тока и напряжения в схеме. Она зависит только от соотношения сопротивлений.
Зная d с, найдем D с и, следовательно, поправку Ñ с:
(3.22)
В.
Значение поправки вносится в результат наблюдения и получается несмещенное значение измеряемого напряжения
; (3.23)
В.
Далее определяются составляющие неисключенных остатков:
d1 = d = 1 % – класс точности приборов;
% – личностная погрешность,
где С – цена деления вольтметра, В/дел.;
% = 0,3 %;
d 3 = di = 0,5% – погрешность внутреннего сопротивления вольтметра;
d 1 ¸ d 3 – инструментальная погрешность;
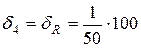% = 2 %– погрешность сопротивления R или модельная погрешность.
Значение результирующей систематической погрешности можно определить по формуле (3.15) заменой si на di.
Расчет по выражению (3.15) проводится для двух значений k: при
Р = 0,95 и Р = 0,99 в связи с тем, что имеются инструментальные и модельные погрешности:
для Р = 0,95
, (3.24)
где коэффициенты bi = 1; m – количество неисключенных остатков,
%;
для Р = 0,99 d рез» 3,2 %.
Далее определяются граничные значения измеряемой величины:
при Р = 0,95 
; 
= 12,3 × 0,025 = 0,31 В;
при Р = 0,99 = 12,3 × 0,032 = 0,40 В.
Результат измерения с округлением:
В при Р = 0,99; 
В при Р = 0,95.
3.1.6. Обработка результатов наблюдений
при наличии случайной погрешности
Погрешность D является случайной величиной. Она может быть представлена в виде:
, (3.25)
где D с – математическое ожидание величины D; 
– случайная величина с нулевым математическим ожиданием.
Неслучайную величину D с называют систематической погрешностью, а – случайной погрешностью. Если значение D с известно, то систематическую погрешность можно исключить, приняв за окончательный результат измерения х испр – исправленный результат измерения.
хиспр = х – Dс. (3.26)
Случайную погрешность исключить нельзя, так как неизвестно, какое конкретное значение приняла случайная величина при данном измерении.
Для оценки влияния погрешности на результат измерения задаются положительными D 1 и D 2 и находят вероятность того, что измеряемая величина х и заключена между (х–D 2) и (х+D 1). Интервал [ х –D2; х +D1] называется доверительным, а вероятность того, что х и находится внутри этого интервала, – доверительной вероятностью Рд. Можно показать, что
Рд = Р [ –D 1 £ D £ D 2]. (3.27)
Обычно выбирают D1 = D2. Тогда
Р д = Р[ |D| £ D1 ]. (3.28)
Если известен дифференциальный закон распределения погрешности D, т. е. плотность вероятности f (D), то
. (3.29)
Числовые характеристики закона распределения f (D) – математическое ожидание D с, дисперсия D и среднее квадратическое отклонение s могут быть определены по формулам:
; (3.30)
; (3.31)
. (3.32)
При нормальном законе распределения погрешностей, пользуясь данными таблицы функции Лапласа Ф(z), можно определить
. (3.33)
При использовании функции Лапласа необходимо учитывать, что
Ф(–z) = –Ф(z). (3.34)
В ряде случаев закон распределения погрешностей неизвестен, однако известны (обычно приближенно) его числовые характеристики Dс и s. Тогда для грубой оценки снизу доверительной вероятности Рд при заданном симметричном доверительном интервале D1 можно воспользоваться неравенством Чебышева:
. (3.35)
откуда
. (3.36)
Если закон распределения погрешностей f (D), а также его числовые характеристики Dс и s неизвестны, то можно определить их приближенно, располагая результатами независимых измерений (наблюдений) одной и той же величины. Приближенные значения величин Dс, s называют оценками.
Если произведено n независимых наблюдений одного и того же известного значения х (например, с целью проверки прибора) и получены результаты х 1, х 2, …, х n, то
; (3.37)
. (3.38)
При неизвестной величине х (произведено n независимых наблюдений одного и того же неизвестного значения) найти оценку систематической погрешности Dс невозможно. Если в рассматриваемом случае можно пренебречь систематической погрешностью, то в качестве оценки истинного значения измеряемой величины следует принять среднее арифметическое результатов наблюдений:
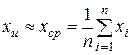. (3.39)
Среднее квадратическое отклонение величины х ср определяется так:
. (3.40)
Среднее квадратическое отклонение каждого отдельного наблюдения, характеризующее точность метода измерения,
. (3.41)
Предполагая, что закон распределения среднего арифметического результатов наблюдений близок к нормальному (имеет место при достаточно большом числе наблюдений), и пренебрегая систематической погрешностью, можно определить
. (3.42)
Если известно, что погрешности отдельных наблюдений распределены по нормальному закону (параметры которого неизвестны), то вместо приближенной формулы (3.37) следует использовать точное выражение:
, (3.43)
где Fn(t) – интегральная функция распределения Стьюдента.
Выражение (3.43) справедливо для любых n, больших единицы.
Если число наблюдений n мало (n < 10¸20), а закон распределения погрешностей отдельных наблюдений нельзя считать близким к нормальному, то применение приближенного выражения (3.42) приводит к значительным погрешностям. В этом случае для грубой оценки величины Рд имеет смысл использовать выражение (3.35), приняв в нем s =sср.
Если случайная величина Y связана с независимыми случайными величинами Y 1, Y 2, …, Yn известной функциональной зависимостью
Y = F(Y 1, Y 2, …, Y n ), то, зная математические ожидания m y1, m y2, …, m yn и средние квадратические отклонения sy 1, sy 2, …, s yn величин Y 1, Y 2, …, Yn, можно приближенно найти математическое ожидание m y и среднее квадратическое отклонение sy величины Y по формулам:
; (3.44)
, (3.45)
где 
– частная производная функции F(y 1, y 2, …, y n ) по yi, взятая в точке (my 1, my 2, …, myn).
Пусть Y 1, Y 2, …, Y n – случайные результаты прямых независимых измерений различных физических величин, а Y = F (Y 1, Y 2, …, Y n) – результат косвенного измерения. Тогда среднее квадратическое отклонение s случайной погрешности результата косвенного измерения можно найти по формуле
, (3.46)
где s i – среднее квадратическое отклонение случайной погрешности результата прямого измерения Yi, а в частности производная берется в точке
y 1, y 2, …, y n, соответствующей результатам прямых измерений.
Систематическая погрешность D с результата косвенного измерения связана с систематическими погрешностями D с1, D с2, …, D сn соответствующих прямых измерений соотношением
. (3.47)
3.2. Задания для самостоятельного решения
3.2.1. Задача № 5. Обработка результатов наблюдений
при однократном измерении
Аналоговым амперметром класса точности d пр с пределом I д и шкалой 150 делений измеряется ток в цепи, содержащей сопротивление R. Сопротивление R имеет погрешность d R, а измерение выполняется при температуре окружающей среды Т окр,оС. Отсчетное устройство показывает N делений с округлением при отсчете до половины деления шкалы. Внутреннее сопротивление амперметра равно R i. Температурная погрешность не превышает значения m основной на каждые D Т, оС.
По данным варианта (табл. 3.2) записать результат измерения.
Температурная погрешность рассчитывается по формуле:
. (3.48)
Таблица 3.2
Исходные данные для задачи № 5
| Заданная величина, размерность | Последняя цифра шифра | |||||||||
| R, Ом | ||||||||||
| Т окр , оС | ||||||||||
| d пр, % | 0,1 | 0,2 | 0,5 | 1,0 | 1,5 | 0,1 | 0,2 | 0,5 | 1,0 | 1,5 |
| N | ||||||||||
| I д,А | 0,5 | 1,5 | ||||||||
| R i, Ом | 0,1 | 0,5 | 0,7 | 0,5 | 0,2 | 3,7 | ||||
| d R,% | 1,0 | 0,5 | 2,0 | 5,0 | 2,0 | 2,0 | 5,0 | 1,0 | 0,1 | 1,0 |
| DТ, оС | ||||||||||
| m | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 1,9 | 1,7 | 1,5 | 1,3 | 1,1 |
