Модуль двоичного счетчика – целая степень числа 2 (М=2n), а его выходное состояние выражается двоичным кодом Qn-1…..Q0, считываемым по выходам триггеров разрядов.
Структуры двоичных счетчиков можно получить по таблицам двоичного счета, либо методам формального синтеза.
Рассмотрим последовательность двоичных чисел от 0 до М-1: для 4-х разрядного счетчика таблицы прямого и обратного счета имеют вид:
| Q3 | Q2 | Q1 | Q0 | |
| Q3 | Q2 | Q1 | Q0 | |
Из таблицы видно, что триггер младшего разряда переключается от каждого входного сигнала (нули и единицы чередуются в Q0 поодиночке).
В следующем разряде – парами, затем четверками, восьмерками и так далее – частота переключений каждого следующего триггера уменьшается вдвое по сравнению с частотой переключений предыдущего.
Следовательно, счетчик можно построить как цепочку последовательно включенных триггеров, каждый из которых обладает свойством деления частоты на два. Однако, это справедливо как для суммирующего, так и для вычитающего счетчиков, нужно дополнительно установить вид связей между триггерами.
В таблице прямого счета соседний старший разряд изменяет состояние при переходе данного разряда из единицы в ноль. Значит суммирующий счетчик – цепочка из триггеров с инверсным динамическим управлением, либо двухступенчатых MS триггеров рассмотренных ранее.
Эквивалент I варианта – цепочка триггеров с прямым динамическим управлением, но сигнал снимается с выхода  .
.
Для схем с обратным счетом из таблицы видно: переключение следующего – при переходе предыдущего из 0 в 1.
Схема вычитающего счетчика – цепочка триггеров с прямым динамическим управлением (либо варианты).
Суммирующие:
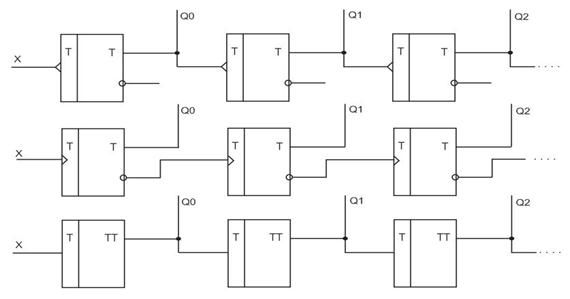
Вычитающие:

Структуры двух счетчиков.
Полученные счетчики называются последовательными (или счетчики с последовательным переносом) – каждый триггер переключается выходным сигналом предыдущего. Временные состязания сигналов отсутствуют – триггеры переключаются поочередно, один за другим.
Максимальное время установления последовательных счетчиков наблюдается при переходах, сопровождающихся переключением всех разрядов (например от 1111 к 0000). Это время пропорционально числу разрядов счетчика и времени переключения триггеров: время установления кода:  ,
, 
В режиме деления частоты быстродействие определяется 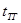 , максимальная входная частота
, максимальная входная частота  (но есть фазовый сдвиг между входной и выходной последовательностями).
(но есть фазовый сдвиг между входной и выходной последовательностями).
В режиме регистрации кода нельзя подавать очередной входной сигнал, пока не зафиксировано предыдущее состояние счетчика, поэтому в таком режиме
 - быстродействие в n раз меньше.
- быстродействие в n раз меньше.
Параллельные (синхронные, с параллельным переносом) счетчики – имеют максимальное быстродействие, поскольку в них все разряды переключаются одновременно.
Добавление единицы к двоичному числу:
 +110111
+110111
 1
1

111000
Результат отличается от исходного числа только в младших разрядах до первого нулевого включительно.
Изменение состоит в инвертировании состояний.
Структура счетчика с параллельным переносом содержит разрядные триггеры и конъюнкторы, анализирующие состояния предыдущих разрядов. При поступлении входного сигнала переключаются только те триггеры, для которых все предыдущие были в единичном состоянии.

Время установления счетчика не зависит от разрядности и равно:
 (
( - конъюнктора).
- конъюнктора).
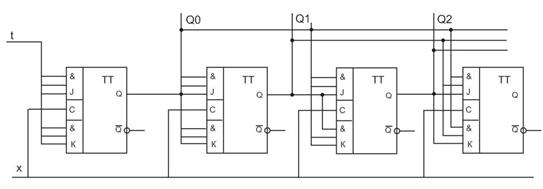
Структурная схема параллельного счетчика на JK-триггерах типа MS (TB1). Конъюнкторы могут отсутствовать если предусмотрены группы входов J и K, связанные по И. В этом случае  .
.
Частотные возможности параллельного и последовательного счетчиков в режиме деления частоты идентичны (если не говорить о фазовых сдвигах).
В параллельных счетчиках все разряды переключаются одновременно, их структуре свойственны временные состязания сигналов. Эти состязания исключаются при использовании MS триггеров.
Обычно разрядность параллельного счетчика ограничена наличием необходимых элементов в используемой серии ИМС. Второе ограничение – рост нагрузки на выходы триггеров по мере увеличения числа разрядов счетчика.
Счетчик с параллельно-последовательным переносом имеет структуру:

Имеет в цепях межгрупповых переносов конъюнкторы, формирующие перенос в следующую группу при единичном состоянии всех триггеров предыдущей.
В наихудшем, с точки зрения быстродействия, случае, когда перенос проходит всю цепь и поступает на вход последней группы, время установления кода:

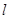 - число групп;
- число групп;
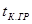 - время установления кода в группе.
- время установления кода в группе.
Если группа – счетчик с параллельным переносом:
 ,
,
Получаем: 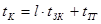
Счетчик со сквозным переносом можно рассматривать как предельный случай группового типа, когда группа является одноразрядной:

Входной сигнал распространяется по цепочке конъюнкторов от младшего разряда до первого, содержащего ноль. Дальнейшее распространение переноса блокируется соответствующим конъюнктором. Распространяясь по цепочке сигнал переноса переключает триггеры и все младшие разряды счетчика, включая первый нулевой, инвертируется, что и требуется для реализации счетного режима.
Максимальное время установки:

По сравнению с последовательным счетчиком схема со сквозным переносом выигрывает в той мере, в какой задержка конъюнктора в данной серии меньше времени распространения в триггере.
Реверсивные счетчики изменяют направление счета под воздействием управляющего сигнала либо при смене точки подачи считаемых сигналов.
В первом случае схема имеет счетный и управляемый входы, во втором – два счетных входа.
Наиболее распространенный способ построения реверсивных счетчиков – переключение межразрядных связей.

В ИМС 155 ИЕ 7 (555) в одном корпусе СИС размещен четырехразрядный параллельный двоичный реверсивный счетчик. Счетчик имеет регулярную структуру, один разряд его:

Схема имеет вход общей установки в нуль (сброс) R, параллельный вход записи D4, тактируемый сигналом С.
По входу прямого счета создается суммирующий счетчик, поскольку работает конъюнктор 1, а 2 блокирован нулевым сигналом, снимаемым с инвертора. При подаче сигналов на вход обратного счета создается вычитающий счетчик, так как точка съема сигнала с триггеров переносится на инверсные выходы (конъюнктор 1 блокирован – на  - единичный сигнал). Инверсии сигналов переноса и заема Р4 и Z4 используются как входные сигналы следующей группы (другой ИМС). Инверторы являются общими и играют роль усилителей – формирователей входных сигналов. Совместное включение 2-х ИМС, дающее 8 разрядный двоичный счетчик (типичен для схем групповых счетчиков с последовательно-параллельным переносом):
- единичный сигнал). Инверсии сигналов переноса и заема Р4 и Z4 используются как входные сигналы следующей группы (другой ИМС). Инверторы являются общими и играют роль усилителей – формирователей входных сигналов. Совместное включение 2-х ИМС, дающее 8 разрядный двоичный счетчик (типичен для схем групповых счетчиков с последовательно-параллельным переносом):

Двоично-кодированные счетчики с произвольным модулем.
Иногда нужны счетчики с модулем счета, не выражаемым целой степенью двойки, то есть произвольным. Такие счетчики реализуются различными способами. Широко распространен и используется в ИМС способ исключения лишних состояний в двоичном счетчике.
Чтобы построить счетчик с модулем К¹2n берут двоичный счетчик с модулем М=2n, так чтобы его разрядность n отвечала условию:  . Разность L=M-K дает число лишних состояний, подлежащих исключению.
. Разность L=M-K дает число лишних состояний, подлежащих исключению.
Способы исключения лишних состояний многочисленны. Исключение в качестве лишних некоторого числа первых состояний счетчика приводит к нулевому начальному состоянию и регистрации в счетчике кода с избытком.
Исключение последних состояний позволяет сохранить естественный порядок счета. Сложность реализации обоих вариантов одинакова.
В счетчиках с исключением последних состояний счет ведется обычным способом вплоть до достижения кода К-1. Далее последовательность переходов счетчика в направлении роста регистрируемого числа должна быть прервана, и следующее состояние должно быть нулевым (при естественном порядке счета). При этом счетчик будет иметь К состояний.
Способ построения счетчиков рассмотрим на примере К=10.
Проведем построение декадного счетчика формализованным путем.
Таблица его функционирования:
| №имп | Исходное состояние | Следующее состояние | ||||||
| Q3 | Q2 | Q1 | Q0 | Q3 | Q2 | Q1 | Q0 | |
Универсальный способ основан на совместном использовании таблиц переходов счетчика и таблиц функционирования триггеров, выбранных для их реализации.
Для JK (который выбираем) таблица функционирования.
| Qt | Qt+1 | J | K |
| X | |||
| X | |||
| X | |||
| X |
| J2 | K2 | QS+1 |
| QS | ||

|
Для Q3:
| Q3 | Q2 | Q1 | Q0 | Q3t | Q3t+1 | Ф-и возбуждения | ||
| J | K | |||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X | ||||||||
| X |
Для J3: Для К3:

J3 = Q0Q1Q2 К3 = Q0.
| Q3 | Q2 | Q1 | Q0 | Q2t+1 | J2 | K2 | Q1t+1 | J1 | K1 | |
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х | |||||||||
| Х | Х |

J2 = Q1Q0;
K2 = Q1Q0;
J1 = Q0  ;
;
K1 = Q0.
Получаем  .
.
Из таблицы видно, что триггер младшего разряда переключается от каждого входного импульса, то есть работает в счетном режиме. Следовательно,  .
.
Зная функции возбуждения триггеров, строим схему:

Часто применяются счетчики с модулем счета М + 1 = 2n + 1. Использование приема увеличения модуля двоичного счетчика на единицу позволяет получить подсхемы, совместное применение которых дает возможность реализовать любой требуемый модуль счета К. Для этого модуль К представляется через слагаемые или множители, каждый из которых легко реализуется (равен М или М + 1). Например, можно использовать представления:
3 = 2 + 1; 5 = 4 + 1; 6 = 3*2; 7 = 6 + 1; 9 = 8 + 1; 11 = 10 + 1; и т.д.
Схему с увеличенным на единицу модулем счета М + 1 можно построить тем же способом, что применен для построения счетной декады. Результат следующий:
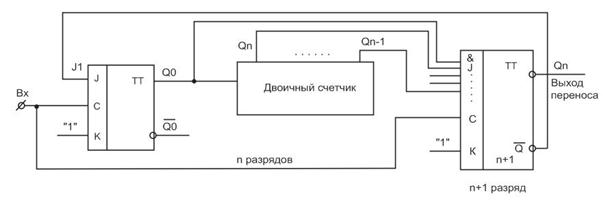
Схема содержит обычный двоичный счетчик в качестве средней части, не включающий первый и последний каскады. В первом и последнем каскадах входы постоянно равны «1», вход J1 получает сигнал в виде перекрестной обратной связи, а вход J последнего триггера получает сигнал в виде конъюнкции входов всех предыдущих триггеров.
При нулевом исходном состоянии схема работает следующим образом. В первом триггере при J1 = 1, а это сохраняется до переключения старшего триггера, осуществляется режим счетного триггера. Пока все предшествующие последнему разряду триггеры не заполнятся единицами, происходит обычный двоичный счет. Такой счет идет до числа 011…11, появление которого открывает группу входов J последнего триггера. После этого состояния возникает состояние: 000…00, так как переключится только последний триггер.
Таким образом, прибавление к некоторому числу разрядов счетчика еще одного разряда здесь приводит к появлению еще одного внутреннего состояния счетчика (в обычном двоичном счетчике это приводит к удвоению числа внутренних состояний).
Для схемы с К = 9 последовательность состояний имеет вид:

Счетчик с К = 9 применяется в схемах контроля и часто используется как часть других счетчиков. Схема в данном случае имеет всего два разряда – первый и последний.

В отечественных и зарубежных сериях имеется счетчик ИЕ 4, используемый как делитель частоты.

На втором и третьем триггерах собрана схема с К = 3. Если подавать входные сигналы на вход 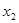 , то получим счетчик с К = 3*2 = 6 по выходу Q4 и счетчик с К = 3 по выходу Q = 3.
, то получим счетчик с К = 3*2 = 6 по выходу Q4 и счетчик с К = 3 по выходу Q = 3.
Если соединить выход Q1 с входом 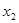 , а входные сигналы подать на вход
, а входные сигналы подать на вход  , то по выходам
, то по выходам  ,
,  ,
,  получаются делители частоты на 2, 6 и 12.
получаются делители частоты на 2, 6 и 12.
Входы  и
и 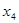 дают управляемую установку нуля, если на один из них подавать управляющий (разрешающий) сигнал, а на второй – тактирующий.
дают управляемую установку нуля, если на один из них подавать управляющий (разрешающий) сигнал, а на второй – тактирующий.






