Управляются несколькими тактовыми последовательностями (то 2 до n).
Из многотактных регистров наибольшее практическое применение получили двухтактные, с основным и дополнительным регистрами, построенными на простых одноступенчатых триггерах.
По такту С1 содержимое основного регистра переписывается в дополнительный, а по такту С2 оно возвращается в основной регистр, но уже в соседние разряды, что соответствует сдвигу слова. По затратам оборудования и быстродействию возникает вариант, идентичный однотактному регистру с двухступенчатыми триггерами.
Рассмотрим один из вариантов использования простого сдвигового регистра в устройствах счета импульсов. Такое использование простого регистра представляет интерес, так как его структурные схемы состоят из повторяющихся триггерных цепей, обладают наращиваемостью и пригодны для различных применений:
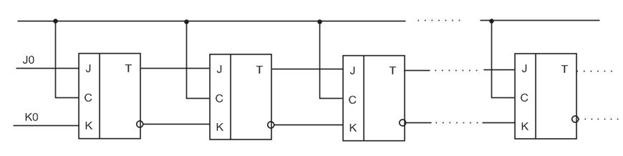
Десятичный счетчик, например, на основе сдвигового регистра, наиболее просто строится с использованием кода Джонсона.
| G | n | n + 1 | ||||||||
| Q0 | Q1 | Q2 | Q3 | Q4 | Q0 | Q1 | Q2 | Q3 | Q4 | |
| a | b | c | d | e | a | b | c | d | e | |
| Избыточные слова: все 5 разрядные числа, где между единицами – нули и наоборот. |
Как видно из таблицы, работа устройства основана на том, что простой пяти разрядный регистр последовательно заполняется единицами (
), а затем – нулями G = 6-9.
Симметричный характер и простота построения таблицы позволяют получить повторяющуюся структурную схему счетчика. Из таблицы видно, что имеется пять независимых переменных a, b, c, d, e, поэтому процедура логического проектирования, рассмотренная выше, будет в данном случае громоздкой.
Используем неформальный, но в ряде случаев эффективный метод составления уравнений входов. Этот метод, основанный на расчленении задачи, дает возможность существенно упростить синтез. Действительно, при счете от нуля до пяти устройство работает как простой сдвиговый регистр, его описывают уравнения:
Эти выражения показывают, что состояние ячейки в (n + 1) такте такое же, как состояние ячейки 
в такте n (аналогично для с и b, d и c, e и d).
Работа устройства при счете 6, 7, 8, 9, как можно видеть, подчиняется тем же выражениям. Разница заключается в том, что в ячейке при G = 6 окажется записанным ноль, а при G = 1 – единица. Процесс записи в ячейку единиц и нулей описывается таблицей:
| n | n + 1 |
| e | a |
И выражением: 
, откуда:
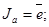
Схема десятичного счетчика имеет вид:
Сравнение полученной структуры с обычным двоично-десятичным счетчиком показывает, что счетчик Джонсона может быть выполнен с помощью меньшего числа корпусов ИМС.
