Схема скользящего резервирования изображена на рисунке 5.9. Вероятность безотказной работы системы для скользящего ненагруженного резервирования замещением при экспоненциальном законе надёжности и при идеальных (безотказных) переключателях находится по формуле [4, 8]
(5.59)
где
λ 0 = n × λJ (5.60)
- интенсивность отказов нерезервированной системы из n элементов; λJ - интенсивность отказов нерезервированного элемента; m 0 – число резервных элементов.
Средняя наработка до отказа системы скользящего резервирования для этого случая равна
Т СК = Т С0 × (m 0 + 1), (5.61)
где Т С0 - средняя наработка до отказа нерезервированной системы.
Если изделие состоит из n основных и одного резервного элемента, находящегося в ненагруженном состоянии, то в течение времени наработки (0.. ti) такое изделие может пребывать в двух несовместных работоспособных состояниях: когда все его элементы (n + 1) работоспособны или когда хотя бы один из них отказывает. В этом случае вероятность безотказной работы изделия Р С(ti) оценивают суммой вероятностей безотказной работы в каждом из этих состояний [1]:
(5.62)
где р (ti), р п(τ) и р (ti - τ) - соответственно вероятности безотказной работы одного (из n) элемента основной системы, переключателя до момента τ включения резервного элемента и резервного элемента с момента τ его включения; f (τ) - плотность распределения наработки до отказа одного элемента основной системы.
При экспоненциальном законе распределения наработки до отказа уравнение (5.62) приобретает вид
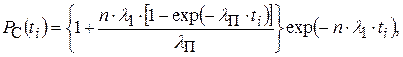(5.63)
где λ 1 и λ П - соответственно интенсивности отказов работающего элемента и переключателя резерва.
